linux 保护 /etc/shadow /etc/group,linux的/etc/passwd、/etc/shadow、/etc/group和/etc/gshadow—关于用户和组的配置文件...

获取数据：

内部数据和外部数据：内部数据比外部数据可靠

一手数据和二手数据：一手数据比二手数据可靠

抽样方法：

概率抽样，例如调查某大学学生跑1000米的成绩

简单随机抽样：去学校随机调查看到的学生

分层抽样：对大一、大二、大三、大四各选取一定数量的学生进行调查

整群抽样：不区分性别，需要对男生和女生都进行调查

系统抽样(等距抽样)：按照一定规则对学号进行抽样，

非概率抽样，主要适用于所需调查的问题不具有普遍性，例如调查某大学学生每周阅读英文杂志的时长

方便抽样：研究者选取自己熟悉的人进行调查

判断抽样：研究者根据自己的判断决定是否对偶一个人进行调查

自愿抽样：被研究者自愿参与调查，自愿抽样在遇到敏感问题时往往会收到比较极端的结果

滚雪球抽样：选取到被调查者，被调查者再推荐满足条件的人参与调查

数据误差

抽样误差

非抽样误差：抽样框误差、回答误差、非回答误差、调查员误差等

Z score标准化

z=(x-μ)/σ，其中x为某一具体数，μ为平均数，σ为标准差

描述统计

集中趋势：平均数、中位数、众数

离散趋势：极值、四分位差

正态分布

若随机变量X服从一个数学期望为μ、方差为σ^2的正态分布，记为N(μ，σ^2)，其概率密度函数为正态分布，期望值μ决定了其位置，标准差σ决定了分布的幅度。当μ = 0、σ = 1时的正态分布是标准正态分布，且 (X-μ)/σ 服从标准正态分布N(0,1)。

根据经验，距均值竖线左右两侧分别1个标准差的竖线，与正太曲线和横坐标轴围起来的面积约为整体面积的68%。

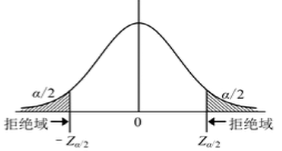
如果X1和X2为两个独立的满足正态分布的样本，则有如下结论。

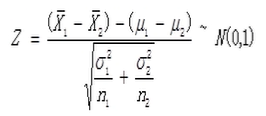
t分布

t-分布(t-distribution)用于根据小样本来估计呈正态分布且方差未知的总体的均值。t分布曲线形态与与自由度df有关，与标准正态分布曲线相比自由度df越小，t分布曲线愈平坦，中间愈低双侧尾部翘得愈高；自由度df愈大，t分布曲线愈接近正态分布曲线；当自由度df=∞时，t分布曲线为标准正态分布曲线，一般为30时从生成的图表上来看基本重合。

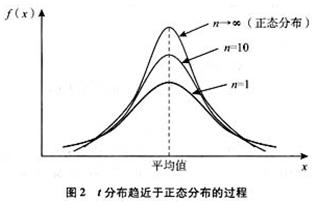
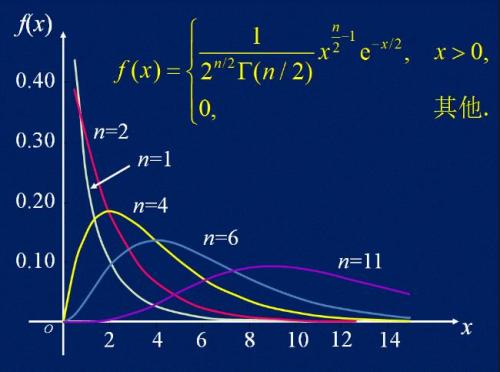
卡方分布

若n个相互独立的随机变量ξ₁，ξ₂，...,ξn服从标准正态分布(也称独立同分布于标准正态分布)，则这n个随机变量的平方和构成一组新的随机变量，其分布规律称为卡方分布(chi-square distribution)，ξ~x2(n)。由于平方过所以卡方分布的值不会小于0.

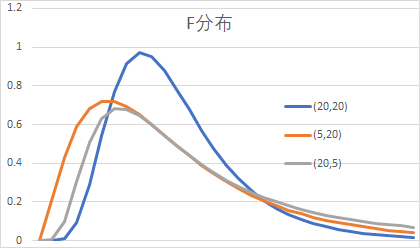
F分布

若总体X~N(0,1)，(X1,X2,...,Xn1)与(Y1,Y2,...,Yn2)为来自X的两个独立样本，即x~x2(n1)，y~x2(n2)，设统计量F=(x/n1)/(y/n2)，则统计量F服从自由度n1和n2的F 分布，记为F~F(n1,n2)

点估计和区间估计

区间估计为[样本均值-一定置信水平下置信度,样本均值+一定置信水平下置信度]

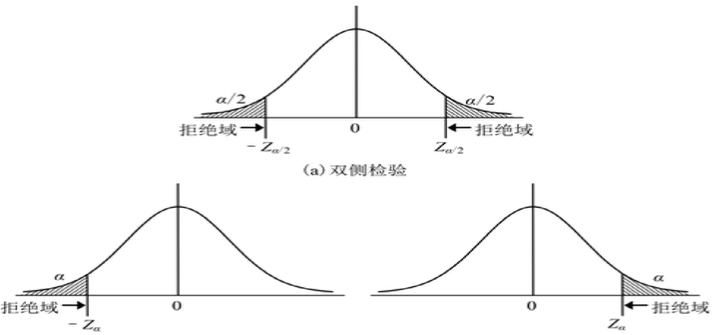
假设检验前提：总体符合正太分布

假设检验原理：

H0：μ=100

H1：μ≠100

对统计样本进行检验，如果P>显著性水平α→H0，P

单因素方差分析

假设检验原理：

H0：xx因素不影响因变量

H1：xx因素影响因变量

几个概念(xij表示样本值，x拔表示每组的样本均值，x拔拔表示所有样本均值，n表示样本数量，k表示组数，)

组内平方和

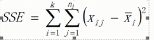
组内均方和

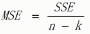
总平方和

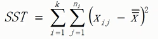
组间平方和

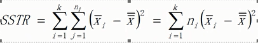
组间均方

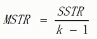
单因素方差分析F值计算

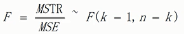
推导SST = SSE + SSTR，即总平方和=组内平方和+组间平方和

DFsst = DFSSE+DFSSTR

无交互因素双因素方差分析

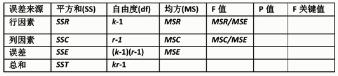
假设检验原理(2套)：

H0：行因素不影响因变量(set1)

H1：行因素显著影响因变量(set1)

H0：列因素不影响因变量(set2)

H1：列因素显著影响因变量(set2)

双因素交互作用

假设检验原理：

H0：行因素和列因素互相独立，无交互作用

H1：行因素和列因素互相影响，有交互作用

线性回归

一元线性回归：一个自变量与因变量的线性关系，形如y = a + bx + e

多元线性回归：多个自变量与因变量的线性关系，形如y = a + b1x1 + b2x2 + ··· + bnxn + e

R square表示因变量有多少可以由自变量解释

对于多元线性回归，即使某一因素对因变量的解释能力很弱，但是如果将其加入模型R2仍然会增加，这就可能会出现虽然R2很高，但其实模型中有一些不太相关的自变量，为了解决这个问题引入了调整R square的概念，Ra2与R2的关系如下，随着R2的增大而增大，随着因变量个数的增加而减小。

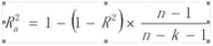
文件/etc/passwd,/etc/shadow,/etc/group

文件/etc/passwd /etc/shadow /etc/group 计算资源的使用(并不是所有的人都可以用这台计算机的) 权限:访问资源的的能力. 用户:获取资源或者权限的凭证. 用户的容器:关 ...

【Linux命令】id，usermod用户管理命令(包括/etc/passwd、shadow、group、gshadow文件)

一.id命令 可以用来查看用户的UID.GID和附加组信息 id会显示用户以及所属群组的实际与有效ID.若两个ID相同,则仅显示实际ID.若仅指定用户名称,则显示目前用户的ID. 1.格式 id [O ...

关于Ubuntu中passwd、shadow、group等文件

在Ubuntu系统中,/etc目录下,有三个文件:passwd shadow group,可能我们已经在用了,但是没有注意到其详细. 这三个配置文件用于系统帐号管理,都是文本文件,可用vi等文本编辑器 ...

用户和用户组管理——passwd、shadow、group、gshadow

在Linux操作系统中,任何一个文件都归属于某一个特定的用户,而任何一个用户都归属于至少一个用户组. 1.用账号文件——passwd 该文件在/etc/passwd 目录下,是保证系统安全的关键文件. ...

Linux中用户与组相关配置文件(整理)

用户与组信息存放位置 说明 注释 /etc/passwd 存放用户基本信息 记录了每个用户的一些基本属性,并对所有用户可读,每一行记录对应一个用户,属性之间通过冒号分隔. 每一个行6个冒号,7个属性. ...

Linux用户和组的配置文件

用户和组的主要配置文件 前两个是放用户账号相关的,后两个是放和组相关的 /etc/passwd:用户及其属性信息(名称.UID.主组ID等) #早期密码也放这里,后来发现不安全,谁都能看 /etc/s ...

passwd、shadow、group文件格式

[root@bogon ~]# cat /etc/passwd root:x:0:0:root:/root:/bin/bash 登录名:密码占位符:UID:GID:注释:家目录:用户的默认shell ...

Linux下的用户、组和权限

目录 一:用户和组信息的查看 查看用户信息 查看密码信息 查看组信息 特殊组wheel 二:用户和组信息的管理 用户管理 组管理 三:文件权限 文件权限的查看 文件权限的修改 ACL控制权限 setf ...

Linux 创建修改删除用户和组

200 ? "200px" : this.width)!important;} --> 介绍 在日常的维护过程中创建用户操作用的相对会多一些,但是在这个过程中涉及到的知识点就 ...

随机推荐

magento后台使用POST表单时，要使用必要参数form_key才能正常通讯

Swift控制语句

前言 Swift提供了类似C语言的流程控制结构,包括可以多次执行任务的for和while循环.还有基于特定条件选择执行不同代码分支的if.guard和switch语句,还有控制流程跳转到其他代码的br ...

图说Java —— 理解Java机制最受欢迎的8幅图

原文链接:  Top 8 Diagrams for Understanding Java 翻译人员: 铁锚 翻译时间: 2013年10月29日 世间总是一图胜过千万言! 下面的8幅图来自于 Progr ...

DB天气 Alpha版使用说明

一 产品介绍 DB天气是一款能够准确预报天气的软件,它的特点在于它的简洁的设计风格,以及贴心的预报方式.是一款非主流的小清新的天气APP. 二 功能介绍 下面介绍一下DB天气的主界面以及天气功能的实现 ...

UIColor，CGColor，CIColor三者间的区别和联系

一.UIColor UIColor是UIKit中存储颜色信息的一个重要的类,一个UIColor对象包含了颜色和透明度的值,它的颜色空间已经针对IOS进行了优化.UIColor包含了一些类方法用于创建一 ...

UIResponder学习

http://blog.youkuaiyun.com/jimzhai/article/details/23283515 UIResponder 介绍 UIResponder 这个类定义了很多用来处理响应和时间处理 ...

css Margin-top塌陷，解决方法

在两个盒子嵌套时,内部的盒子设置的margin-top会加到外边的盒子上,导致内部的盒子margin-top设置失败,解决方法如下: (1)外部盒子设置一个边框 (2)外部盒子设置overflow:h ...

Oracle 更改字符集 更改后之前的中文全成乱码了

安装时采用什么字符集主要看你的需求,一般测试用的话,就用UTF8.后面可以修改, 10g:UTF8 到ZHS16GBK SHUTDOWN IMMEDIATE; STARTUP MOUNT ; ALTE ...