本文详细介绍了二叉排序树（BST）的概念及其特性，包括插入、删除和查询等基本操作的实现。在插入过程中，如果节点已存在则直接返回，否则找到合适位置插入新节点。删除操作分为三种情况：无子节点、单子节点和双子节点，每种情况都有相应的处理方式。查询操作通过比较关键字与节点值进行，时间复杂度在最好和最坏情况下分别为O(logn)和O(n)。最后，文章展示了二叉排序树的中序遍历方法。
二进制排序树(BST)，也称为二进制搜索树或空树；或具有以下属性的二叉树:
(1)如果其左子树不为空，则左子树上所有节点的值都小于其根节点的值;
(2)如果右子树不为空，则右子树中所有节点的值都大于其根节点的值；
(3)它的左和右子树也是二进制排序树.
二进制排序树是动态树表. 它的特点是不会一次生成树的结构，而是在搜索过程中
二进制排序树的操作包括插入，删除，查询和遍历.
注意: 二进制排序树中没有具有相同值的节点
a. 插入过程相对简单. 首先确定要插入的值在二进制排序树中是否已经存在. 如果已经存在，则直接返回；如果不存在，请转到b;
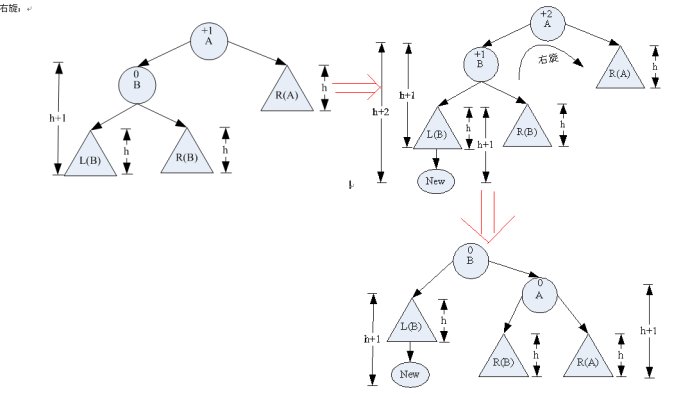
b. 当前要插入的值不存在，您应该找到合适的位置并将其插入. 请注意，插入的新节点必须是叶节点；
a. 与插入类似，要删除具有给定值的节点二叉排序树算法，请首先确定该节点是否存在(如果尚不存在)，然后直接返回；如果已经存在，则获取给定值的节点的位置，根据不同的Delete进行调整，转到b；
b. 如果要删除的节点只有左子树(只有右子树)，则直接将要删除的节点的左子树(右子树)放在要删除的节点位置，并释放该节点的内存要删除，否则转到c;
c. 如果要删除的节点同时具有左和右子树，则此时的删除可能会有些复杂，但也更易于理解. 将在要删除的节点的左子树中找到最大值最大的节点，并将其放置在要删除的节点的位置.
查询过程相对简单. 首先，将关键字与根节点的关键字进行比较. 如果它们相等，则返回节点(指针)的位置；否则，返回0. 否则，如果根节点的关键词小于，则在左子树中继续搜索. 如果关键字大于根节点，则转到右侧子树查找；如果找不到叶节点，则返回NULL.
查询过程中的最佳情况如上图所示，节点均匀分布在左右子树中，搜索时间复杂度为O(logn)；最坏的情况是构建二进制排序树. 这时，输入关键字序列才刚刚排序. 此时形成的二进制排序树是单分支二进制树. 此时，搜索退化为单链列表搜索，时间复杂度为O(n). 图:
从以上两个排序树的定义中可以看出，左子树的所有值均小于根节点，右子树的所有值均大于根节点，这功能与二叉树的中阶遍历完全相同-左子树->根节点->右子树重合，因此二叉树的中阶遍历恰好是一个顺序
#include
#include
//二叉排序树
typedef struct BSTNode
{
int data;
BSTNode *lchild; //左孩子
BSTNode *rchild; //右孩子
}BSTNode, *BSTree;
bool Search(BSTree bst, int key, BSTree f, BSTree *p);
void InOderTraverse(BSTree bst) //中序递归遍历二叉树
{
if (NULL != bst)
{
InOderTraverse(bst->lchild);
printf("%d ", bst->data);
InOderTraverse(bst->rchild);
}
}
static BSTNode* BuyNode(int data) //生成一个节点并进行初始化
{
BSTNode *pTmp = (BSTNode*)malloc(sizeof(BSTNode));
if (NULL == pTmp)
{
exit(0);
}
pTmp->data = data;
pTmp->lchild = NULL;
pTmp->rchild = NULL;
return pTmp;
}
bool Insert(BSTree *bst, int key)
{
if (NULL == *bst) //空树
{
*bst = BuyNode(key); //插入根节点
return true;
}
BSTNode *p;
//先在二叉排序树中查找要插入的值是否已经存在
if (!Search(*bst, key, NULL, &p)) //如果查找失败，则插入；此时p指向遍历的最后一个节点
{
BSTNode *pNew = BuyNode(key);
if (key < p->data) //将s作为p的左孩子
{
p->lchild = pNew;
}
else if (key > p->data) //将s作为p的右孩子
{
p->rchild = pNew;
}
return true; //插入成功
}
else
{
printf("\nThe node(%d) already exists.\n", key);
}
return false;
}
/*
删除分三种情况：
(1)被删除的节点无孩子，说明该节点是叶子节点，直接删
(2)被删除的节点只有左孩子或者右孩子，直接删，并将其左孩子或者右孩子放在被删节点的位置
(3)被删除的节点既有右孩子又有右孩子
*/
BSTNode* FindParent(BSTree bst, BSTNode *child)
{
if (NULL == bst)
{
return NULL;
}
if (bst->lchild == child || bst->rchild == child)
{
return bst;
}
else if(NULL != bst->lchild)
{
FindParent(bst->lchild, child);
}
else if (NULL != bst->rchild)
{
FindParent(bst->rchild, child);
}
}
void Delete(BSTree *bst, int key)
{
if (NULL == *bst)
{
exit(1); //空树直接报错
}
BSTNode *p;
BSTNode *f = NULL;
BSTNode *q, *s;
if (Search(*bst, key, NULL, &p)) //确实存在值为key的节点,则p指向该节点
{
if (NULL == p->lchild && NULL != p->rchild) //无左孩子,有右孩子
{
q = p->rchild;
p->data = q->data; //因为两个节点之间本质的不同在于数据域的不同，而与放在哪个地址没有关系
p->rchild = q->rchild;
p->lchild = q->lchild;
free(q);
}
else if (NULL == p->rchild && NULL != p->lchild) //无右孩子,有左孩子
{
q = p->lchild;
p->data = q->data;
p->rchild = q->rchild;
p->lchild = q->lchild;
free(q);
}
else if (NULL != p->rchild && NULL != p->lchild) //既有左孩子，又有右孩子
{
q = p;
s = p->lchild; //找左孩子的最右孩子
while (s->rchild)
{
q = s;
s = s->rchild;
}
p->data = s->data;
if (q != p)
{
q->rchild = p->lchild;
}
else
{
q->lchild = s->lchild;
}
free(s);
}
else
{
if (*bst == p) //只有一个根节点
{
free(*bst);
*bst = NULL;
return;
}
BSTNode* parent = FindParent(*bst, p);
if (parent->lchild == p)
{
parent->lchild = NULL;
}
else
{
parent->rchild = NULL;
}
free(p);
}
}
}
bool Search(BSTree bst, int key, BSTree f, BSTree *p) //查找成功时，p指向值为key的节点。如果查找失败，则p指向遍历的最后一个节点
{
if (!bst)
{
*p = f;
return false;
}
if (bst->data == key) //查找成功，直接返回
{
*p = bst;
return true;
}
else if (bst->data < key)
{
return Search(bst->rchild, key, bst, p);
}
return Search(bst->lchild, key, bst, p);
}
int main(void)
{
BSTNode *root = NULL;
Insert(&root, 45);
Insert(&root, 24);
Insert(&root, 53);
Insert(&root, 12);
Insert(&root, 90);
InOderTraverse(root);
printf("\n%d ", Insert(&root, 45)); //输出0表示插入失败，输出1表示插入成功
printf("%d\n", Insert(&root, 4));
InOderTraverse(root);
printf("\n");
Delete(&root, 4); //删除节点45
Delete(&root, 45); //删除节点45
Delete(&root, 24); //删除节点45
Delete(&root, 53); //删除节点45
Delete(&root, 12); //删除节点45
Delete(&root, 90); //删除节点45
InOderTraverse(root);
return 0;
}
运行结果:
本文来自电脑杂谈，转载请注明本文网址：
http://www.pc-fly.com/a/jisuanjixue/article-272789-1.html
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
