路径规划 | 基于粒子群算法的栅格地图机器人路径规划（Matlab）-优快云博客

效果一览

路径规划 | 基于粒子群算法的栅格地图机器人路径规划（Matlab）_机器人路径规划

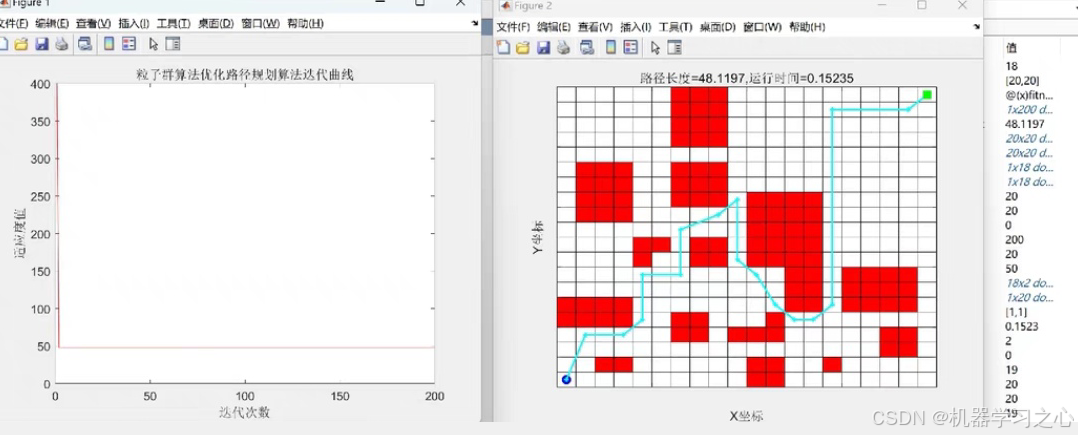
基本介绍

路径规划 | 基于粒子群算法的栅格地图机器人路径规划（Matlab）
粒子群算法(PSO)是一种基于群体智能的优化算法，广泛应用于路径规划、机器学习和数据挖掘等领域。Matlab是一种强大的数学软件，提供了丰富的机器学习和优化工具箱，可以方便地实现PSO算法。
路径规划方面，PSO算法可以帮助我们寻找最优路径，从而提高导航系统的准确性和效率。

程序设计

完整源码和数据私信博主回复基于蜣螂优化算法的栅格地图机器人路径规划（Matlab）

clc
clear
close all

%% 输入数据
G=[ 0 0 1 1 1 0 0 0 0 1
    1 0 0 0 0 0 0 0 0 0
    0 0 0 0 0 0 0 0 0 0
    0 1 1 0 1 0 0 0 0 0
    0 1 1 0 1 0 0 0 1 0
    0 0 0 0 0 0 1 0 0 0
    0 0 0 1 0 0 0 0 0 1
    0 0 0 0 0 0 1 1 0 0
    0 1 0 0 0 0 1 0 0 0
    0 1 0 0 1 0 0 0 0 0];
% G=[ 0 1 1 1 0 
%     1 0 0 0 0 
%     0 0 0 0 1 
%     0 0 0 0 1 
%     0 1 1 0 1];


G = zeros(10,10);
d = randperm(95,21)+1;
d=sort(d);
G(d) = 1;

%% 栅格绘制
drawShanGe(G,0)
title('栅格地图')
%%
S = [1 1];    % 起点
E = [10 10];  % 终点
G0 = G;
G = G0(S(1):E(1),S(2):E(2)); % 该方式是为了方便更改起点与终点
[Xmax,dim] = size(G);        % 栅格地图列数为粒子维数，行数为粒子的变化范围
dim = dim - 2;               % 减2是去掉起点与终点

%% 参数设置
maxgen = 50;    % 最大迭代次数
NP = 30;         % 种群数量

%%%%%%%%%%%%%%%%%%%%%%%%%%%
 rPercent = 0.2;    

%%%%%%%%%%%%%%%%%%%%%%%%%%%
pNum = round( NP * rPercent );    % %发现者



Xmin = 1;   % 变量下界

%% 初始化
X = zeros(NP,dim);
for i = 1:NP
    for j = 1:dim
       col = G(:,j+1);      % 地图的一列
       id = find(col == 0); % 该列自由栅格的位置
       X(i,j) =  id(randi(length(id))); % 随机选择一个自由栅格
       id = [];
    end 
    fit( i ) = fitness(X( i, : ),G);
end
fpbest = fit;   % 个体最优适应度
pX = X;      % 个体最优位置
 XX=pX;
[fgbest, bestIndex] = min( fit );        % 全局最优适应度
bestX = X(bestIndex, : );    % 全局最优位置
[fmax,B]=max(fit);
worse= X(B,:);  
%%
for gen = 1 : maxgen
    gen

       [ ans, sortIndex ] = sort( fit );% Sort.
     
      [fmax,B]=max( fit );
       worse= X(B,:);  
        
        [~, Idx] = sort( fpbest );
  r2=rand(1);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
for i = 1 : pNum
 if(r2<0.9)
            r1=rand(1);
          a=rand(1,1);
          if (a>0.1)
           a=1;
          else
           a=-1;
          end
    X( i , : ) =  pX(  i , :)+0.3*abs(pX(i , : )-worse)+a*0.1*(XX( i , :)); % Equation (1)
       else
            
           aaa= randperm(180,1);
           if ( aaa==0 ||aaa==90 ||aaa==180 )
            X(  i , : ) = pX(  i , :);   
           end
         theta= aaa*pi/180;   
       
       X(  i , : ) = pX(  i , :)+tan(theta).*abs(pX(i , : )-XX( i , :));    % Equation (2)      

      end
          X( i , :) = Bounds(X(i , : ), Xmin, Xmax );
         fit(  i  ) = fitness( X(  i , : ),G );
    end 
 [ fMMin, bestII ] = min( fit );      
  bestXX = X( bestII, : );  
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
 R=1-gen/maxgen;                           %
 %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
 Xnew1 = bestXX.*(1-R); 
     Xnew2 =bestXX.*(1+R);                    %%% Equation (3)
   Xnew1= Bounds(Xnew1, Xmin, Xmax );
   Xnew2 = Bounds(Xnew2, Xmin, Xmax );
 %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
     Xnew11 = bestX.*(1-R); 
     Xnew22 =bestX.*(1+R);                     %%% Equation (5)
   Xnew11= Bounds(Xnew11, Xmin, Xmax );
   Xnew22 = Bounds(Xnew22, Xmin, Xmax );
   
   
     for i = ( pNum + 1 ) :12                  % Equation (4)
     X( i, : )=bestXX+((rand(1,dim)).*(pX( i , : )-Xnew1)+(rand(1,dim)).*(pX( i , : )-Xnew2));
    X( i , :) = Bounds(X(i , : ),  min(Xnew1), max(Xnew2) );
   fit(  i  ) = fitness( X(  i , : ),G );
   end
   
  for i = 13: 19                  % Equation (6)

   
        X( i, : )=pX( i , : )+((randn(1)).*(pX( i , : )-Xnew11)+((rand(1,dim)).*(pX( i , : )-Xnew22)));
       X( i , :) = Bounds(X(i , : ), Xmin, Xmax );
         fit(  i  ) = fitness( X(  i , : ),G );
  
  end
  
  for j = 20 : NP                 % Equation (7)
       X( j,: )=bestX+randn(1,dim).*((abs(( pX(j,:  )-bestXX)))+(abs(( pX(j,:  )-bestX))))./2;
      X( j , :) = Bounds(X(j , : ), Xmin, Xmax );
         fit(  j  ) = fitness( X(  j , : ),G );
  end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% 
     XX=pX;
    %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
    % 更新个体最优值和全局最优值
    for i = 1 : NP
        if (fit(i) < fpbest(i))
            fpbest(i) = fit(i);
            pX(i, :) = X(i, :);
        end
        if(fpbest(i) < fgbest)
            fgbest = fpbest(i);
            bestX = pX(i, :);
        end
    end
    bestX = LocalSearch(bestX,Xmax,G);
    fgbest = fitness(bestX,G);
    FG(gen,1)=fgbest;
end