[leetcode]64. Minimum Path Sum

原创于 2018-12-07 11:35:08 发布 · 147 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#leetcode

LeetCode 同时被 3 个专栏收录

336 篇文章

订阅专栏

Medium

162 篇文章

订阅专栏

23 篇文章

订阅专栏

本文深入解析了LeetCode题目64：最小路径和的解决方案，采用动态规划方法，详细介绍了如何从二维矩阵中找到从左上角到右下角的最小路径和。同时，提供了两种实现方式，包括原始的二维动态规划和优化后的空间复杂度降低的一维动态规划。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

[leetcode]64. Minimum Path Sum

Analysis

好冷鸭~会下雪么—— [每天刷题并不难0.0]

Given a m x n grid filled with non-negative numbers, find a path from top left to bottom right which minimizes the sum of all numbers along its path.
Note: You can only move either down or right at any point in time.
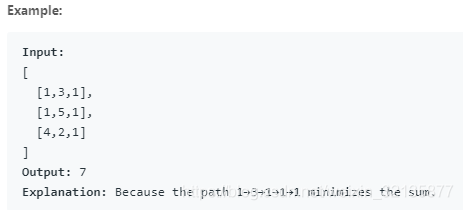
在这里插入图片描述
简单的动规~

Implement

class Solution {
public:
    int minPathSum(vector<vector<int>>& grid) {
        int m = grid.size();
        int n = grid[0].size();
        vector<vector<int>> dp(m, vector<int>(n, grid[0][0]));
        for(int i=1; i<m; i++)
            dp[i][0] = dp[i-1][0]+grid[i][0];
        for(int j=1; j<n; j++)
            dp[0][j] = dp[0][j-1]+grid[0][j];
        for(int i=1; i<m; i++){
            for(int j=1; j<n; j++)
                dp[i][j] = min(dp[i-1][j], dp[i][j-1])+grid[i][j];
        }
        return dp[m-1][n-1];
    }
};

可以对上面的dp[][]做一下优化，减少空间复杂度

class Solution {
public:
    int minPathSum(vector<vector<int>>& grid) {
        int m = grid.size();
        int n = grid[0].size();
        vector<int> dp(m, grid[0][0]);
        for(int i=1; i<m; i++)
            dp[i] = dp[i-1]+grid[i][0];
        for(int j=1; j<n; j++){
            dp[0] += grid[0][j];
            for(int i=1; i<m; i++){
                dp[i] = min(dp[i], dp[i-1]) + grid[i][j];
            }
        }
        return dp[m-1];
    }
};