时间序列分解
大量时间序列的观测样本表现出趋势性、季节性和随机性,或者三者中的其一或其二。于是,我们认为每个时间序列,都可以分为三个部分的叠加
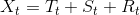
其中,T是趋势项,S是季节项,R是随机项。
上述公式表现了趋势项和季节项是累加的,实际应用场景中,趋势项和季节项可能是累乘的,时间序列可以分解为如下公式
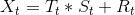
实际应用中,随机项R的期望为0,没有规律,并且绝对值不大。所以在应用场景中我们往往省略掉R,R称作噪声。预测公式如下
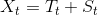
或
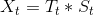
一次指数平滑法
线性回归算法中,每个经验点的权重是一致的,即很早以前的经验数据也可能对预测数据有较大的影响。很多实际场景中,未来一段时间的趋势可能和在最近一段时间的趋势关系更加紧密。比如小明去年数学考试成绩一直不及格,今年连续多次考试90多分,预测小明下一次数学考试的成绩,情理上90多分的可能性更高。采用传统的线性回归算法,预测结果可能是70多分。
指数平滑法认为越老的经验数据对趋势的影响越小。我们假定时间t的观测值为y(t),时间t的预测值为S(t),则时间t+1的预测值S(t+1)为
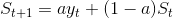
a的取值范围(0, 1),a越大,最近时间点的观测值对预测值的影响越大。
假设我们有t个经验数据,根据上述一次指数平滑公式,预测值S(t + n) = S(t + 1),预测值不具备趋势。
二次指数平滑
我们对一次指数平滑值再进行指数平滑,可以获得趋势。二次指数平滑法的预测模型为:
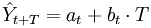
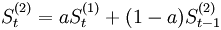





 本文介绍了时间序列分析中的三次指数平滑法,包括一次、二次和三次指数平滑的原理及应用。重点讨论了带有季节性的Holt-Winters算法,解释了其趋势项和周期项的计算,并给出了Java实现代码,但指出代码存在预测公式逻辑错误。
本文介绍了时间序列分析中的三次指数平滑法,包括一次、二次和三次指数平滑的原理及应用。重点讨论了带有季节性的Holt-Winters算法,解释了其趋势项和周期项的计算,并给出了Java实现代码,但指出代码存在预测公式逻辑错误。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 1797
1797

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








