【深度学习】3层神经网络的BP推导

先来复习一下理论：

简述反向传播原理【baba】，这道题忽然发现自己根本什么都说不出口。。。

思路具体是先介绍前向传播，再介绍反向传播。

在多层感知机中，输入信号通过各个网络层的隐节点产生输出的过程称为前向传播。在网络训练中，前向传播最终产生一个标量损失函数，反向传播算法BP则是将损失函数的信息沿网络层向后传播用以计算梯度，达到优化网络参数的目的。

反向传播的理解  西瓜书p101

神经网络——BP算法 

如何直观地解释 backpropagation 算法？

随机一些权重，输入*权重之后求和，得到下一层每个节点的输入；经过激活函数，得到该层的输出；然后继续向下一层传播，直到输出。

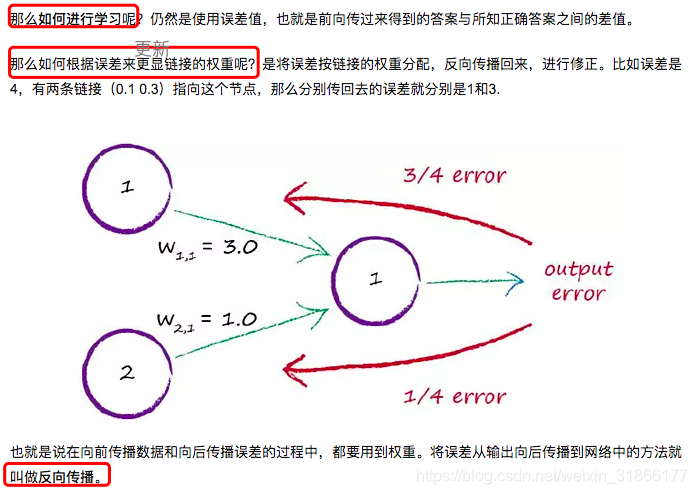
反向传播——将误差从输出向后传播到网络中的方法

---

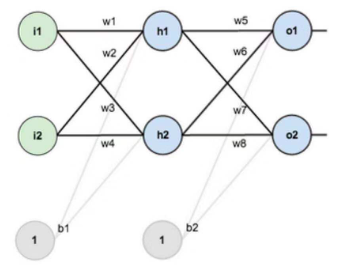
三层神经网络的前馈过程： 

损失函数为MSE（均方误差函数）：

BP反向传播过程：

对于输出层，想知道其改变对总误差有多少影响，于是得：

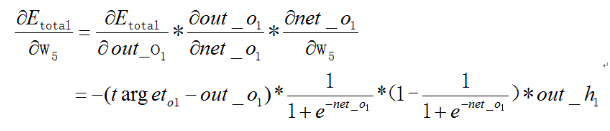
同理，W_5,6,7,8都能计算出更新的结果。

对于隐藏层W_1（注：在求W1的时候用到了W5的值，这时候还用的是W5的原始值!不是bp更新的值！！）

---

解决梯度消失问题

使用ReLU。

使用ReLU 函数时：gradient = 0 (if x < 0), gradient = 1 (x > 0)。不会产生梯度消失问题。、

注：实际上就是梯度计算过程中，w值和激活函数的导数值相乘大于1或者小于1的问题，如果是大于1，那么经历过很多个隐藏层梯度就会越来越大，即梯度爆炸，如果是小于1当然就是梯度消失啦。

---

参考：

深度学习---反向传播的具体案例 (这里有详细的数值计算过程~！;-))

三层神经网络的bp算法详细推导过程

深度学习 — 反向传播(BP)理论推导 （前几张图很直观的展示了反向传播，后面emmm）