使用Ruby进行时间序列异常检测的实用指南

本文还有配套的精品资源，点击获取

简介：时间序列数据分析是统计学的一个重要分支，尤其在大数据和机器学习中非常重要。本项目展示了如何使用Ruby编程语言检测时间序列数据中的异常值。时间序列数据是按时间顺序排列的一组数据点，如股票价格或网站访问量等，并可能展现趋势性、季节性和周期性特征。异常值可能由错误、异常情况或罕见事件引起，对分析结果影响重大。在本项目中，我们基于正态分布假设，采用Z-score和IQR方法来识别异常。开发者需要预处理数据，并可能调整方法以适应特定场景。

1. 时间序列数据分析基础

在数据分析的众多分支中，时间序列分析因其独特性占据了一席之地。它主要研究在不同时间点上采集的数据序列，用以挖掘数据随时间变化的规律性。理解时间序列的基本特征对于进行深入的异常检测和预测分析至关重要。在时间序列分析中，数据通常具有以下特点：时间依赖性、季节性、趋势性和周期性。正确理解并处理这些特性，能够帮助我们在识别异常、构建预测模型时做出更为科学的决策。

本章将首先介绍时间序列分析的基本概念和关键术语，然后逐步深入探讨如何识别和处理数据中的异常值。通过这些基础知识的铺垫，读者可以更好地理解后续章节中关于异常值处理和正态分布应用的讨论。此外，为使读者能够将理论知识应用于实践，我们还会提供一些常用的数据分析工具和方法，并通过案例展示如何在实际工作中应用这些理论。

## 1.1 时间序列数据的特性
时间序列数据通常包括以下四种基本特性：

- **时间依赖性**: 数据点之间存在随时间变化的依赖关系。
- **趋势性**: 数据集随时间表现出的总体上升或下降的趋势。
- **季节性**: 数据在特定时间段内重复出现的模式。
- **周期性**: 数据表现出的非固定时间间隔的重复模式。

在进行时间序列分析时，了解这些特性有助于选择合适的方法和算法，对于后续的异常检测和预测至关重要。

从下一章开始，我们将具体探讨异常值的概念及其对数据分析的影响，并学习不同的异常值识别和处理方法。

2. 异常值的识别与处理

2.1 异常值的概念及其影响

2.1.1 异常值定义

异常值是指在数据集中，那些与大部分数据显著不同的数据点。它们可能是由于测量误差、数据输入错误、或者真实的变化导致的。异常值的识别对于数据分析至关重要，因为它可以揭示数据集中的特殊问题，或是反映潜在的问题和机遇。

2.1.2 异常值对数据分析的影响

异常值的存在会严重影响数据分析的结果。在计算均值和方差时，异常值可能导致这些统计量的偏移，进而影响到假设检验、模型构建等后续的数据分析步骤。例如，在机器学习模型中，异常值可能被模型过度重视，从而导致过拟合，降低模型的泛化能力。

2.2 异常值的识别方法

2.2.1 视觉识别法

视觉识别法包括绘制箱线图、直方图、散点图等，通过图形化的方法来识别异常值。比如，箱线图能直观展示数据的分布情况，超过上下四分位数1.5倍的极值通常被认为是异常值。

2.2.2 统计测试法

统计测试法利用概率论和统计学原理来识别异常值，如格拉布斯检验（Grubbs’ Test）和狄克逊Q检验（Dixon’s Q Test）。这些方法通过计算出一个统计量，并与临界值进行比较，超过临界值的点被认为是异常值。

2.2.3 机器学习法

机器学习法借助算法模型识别异常值，例如孤立森林（Isolation Forest）、局部异常因子（Local Outlier Factor, LOF）等算法。这些模型通常需要在正常数据集上进行训练，然后用来识别未知数据中的异常值。

2.3 异常值的处理方法

异常值的处理方法很多，包括删除、替换、变换、修正等。在删除方法中，可以基于统计测试或视觉识别结果删除异常值。替换是指用统计学上代表性的值如均值、中位数来替代异常值。变换和修正方法则更多地用于调整数据的尺度或形态，减少异常值对分析的影响。

2.4 本章节的图示和代码实现

2.4.1 可视化异常值识别

为了通过可视化识别异常值，我们首先绘制一个箱线图：

import matplotlib.pyplot as plt
import numpy as np

# 创建一个包含异常值的数据集
data = np.concatenate([np.random.normal(0, 1, 100), np.random.normal(10, 1, 10)])

# 绘制箱线图
plt.figure(figsize=(8, 4))
plt.boxplot(data, vert=False)
plt.title('Boxplot to Identify Outliers')
plt.xlabel('Data Values')
plt.show()

上述代码块生成了一个包含正常数据和异常数据的箱线图，正常数据大约在0附近分布，而异常数据在10附近。异常数据点通常被定义为超出箱子边界的点。

2.4.2 统计测试法示例代码

下面的Python代码使用了Grubbs检验来检测数据中的异常值：

from scipy.stats import t
import numpy as np

def grubbs_test(data, alpha=0.05):
    n = len(data)
    max_val = np.max(data)
    min_val = np.min(data)
    G = np.max(np.abs([max_val - np.mean(data), np.mean(data) - min_val])) / (0.5 * (max_val - min_val))

    t_val = (n - 1) * np.sqrt(G**2 / (n**2 - G**2))
    critical_value = (n - 1) / np.sqrt(n) * np.sqrt((t.ppf((1 + alpha) / 2, n - 2) ** 2) / (n - 2 + (t.ppf((1 + alpha) / 2, n - 2) ** 2)))

    return t_val, critical_value

# 示例数据集
data_set = [1, 2, 3, 4, 5, 120]

# 执行Grubbs检验
t_stat, crit_val = grubbs_test(data_set)

print(f"Test statistic G: {t_stat}")
print(f"Critical value: {crit_val}")

if t_stat > crit_val:
    print("Outlier detected")
else:
    print("No outlier detected")

此代码将检测给定数据集中的异常值，通过与临界值的比较来确定是否有异常值存在。

通过本章节的介绍，我们了解到识别和处理异常值在数据分析中的重要性，并且学会了使用几种实用的方法和技巧。接下来的章节将探讨正态分布的概念及其在数据分析中的应用。

3. 正态分布概念及应用

3.1 正态分布基础

正态分布是数据分析中的核心概念，尤其在处理异常值和数据建模时，其重要性不容忽视。本章节将从正态分布的定义出发，探讨其性质和在异常值识别中的应用。

3.1.1 正态分布的定义和性质

正态分布，也称高斯分布，是连续概率分布的一种，由德国数学家卡尔·弗里德里希·高斯提出。其概率密度函数在数学上表现为关于均值对称的钟形曲线，其方程为：

f(x | μ, σ^2) = (1 / sqrt(2πσ^2)) * exp(- (x - μ)^2 / (2σ^2))

其中，μ 表示分布的均值，σ^2 表示方差，σ 为标准差。正态分布具有几个显著的性质：

• 对称性：均值左右对称。
• 单峰性：概率密度函数有一个峰值，即均值所在点。
• 均值、中位数和众数重合。
• 大约 68% 的数据落在距离均值一个标准差的区间内，95% 落在两个标准差内，99.7% 落在三个标准差内。

3.1.2 正态分布与异常值的关系

由于正态分布的这些性质，我们常利用正态分布来识别异常值。在正态分布的数据集中，偏离均值较远的点出现的概率较小，因此可以认为这些点可能是异常值。一般而言，当数据点偏离均值超过三个标准差（+/- 3σ）时，这样的点通常会被视为潜在的异常值。

3.2 正态分布的应用场景

正态分布在多个领域有广泛的应用，以下将探讨其在工业质量控制和金融风险评估中的应用。

3.2.1 工业质量控制

在制造业和工业生产中，质量控制至关重要。正态分布用于监控生产线上的产品质量。借助正态分布的性质，可以设定质量控制的上下限，超出这个范围的数据点可以视为不合格产品，需要进一步检查或剔除。例如，对于一个生产汽车轮胎的工厂，如果轮胎的直径服从正态分布，那么通过设定合理的均值和标准差，可以有效地控制轮胎质量，从而减少不合格品率。

3.2.2 金融风险评估

金融领域是正态分布应用的另一个重要场景。在金融风险管理中，正态分布可以帮助评估投资组合的收益风险。资产的收益往往假定为正态分布，其波动性可以通过标准差来衡量。银行和金融机构使用正态分布模型来预测市场风险，并据此设定资本准备金。例如，在计算潜在的损失时，金融机构会用正态分布来估计在不同置信水平下的潜在损失额。

为了展示正态分布的应用，我们可以用Mermaid图表展示一个正态分布曲线的例子：

graph LR
    A[开始] --> B{确定均值μ和标准差σ}
    B --> C[计算Z分数]
    C --> D[将Z分数转换为概率]
    D --> E[绘制正态分布图]
    E --> F[分析概率密度函数]
    F --> G[识别异常值]
    G --> H[结束]

在本章节中，我们详细介绍了正态分布的基础知识及其在工业和金融领域中的应用，为后面章节中介绍的具体异常值检测方法奠定了理论基础。在下一章节中，我们将深入探讨两种重要的异常值检测方法：Z-score和IQR。

4. Z-score与IQR异常检测方法

4.1 Z-score方法详解

4.1.1 Z-score的计算公式

Z-score是一种用于统计学中的标准化数据的方法，它基于原始数据值和总体平均值之间的差异，并根据标准差来衡量这种差异。计算公式如下：

[ Z = \frac{(X - \mu)}{\sigma} ]

其中，(X)代表原始数据点，(\mu)代表数据集的平均值，而(\sigma)代表数据集的标准差。一个数据点的Z-score值表明了该数据点距离平均值的标准差数。如果一个数据点的Z-score绝对值大于3，通常认为这个点是异常的。

4.1.2 Z-score在异常检测中的应用

在异常检测中，Z-score方法通过计算数据点的Z-score值来识别异常。这是因为大多数分布呈现钟形曲线，大部分数据集中在平均值附近，而远离平均值的数据点可能表示异常情况。通过设定阈值（如Z-score绝对值大于3），我们可以有效识别出异常值。

下面是一个简单的Python代码示例来计算Z-score值：

import numpy as np

def calculate_z_scores(data):
    # 计算平均值和标准差
    mean = np.mean(data)
    std = np.std(data)
    # 计算Z-score
    z_scores = (data - mean) / std
    return z_scores

# 示例数据
data = np.array([1, 2, 3, 4, 100])

# 计算并打印Z-scores
z_scores = calculate_z_scores(data)
print("Z-scores for the data:", z_scores)

在上述代码中，首先计算了数据集的平均值和标准差。然后，使用这些值来计算每个数据点的Z-score。结果中，任何绝对值大于3的Z-score都可能指示一个异常值。

4.2 IQR方法详解

4.2.1 IQR的概念和计算

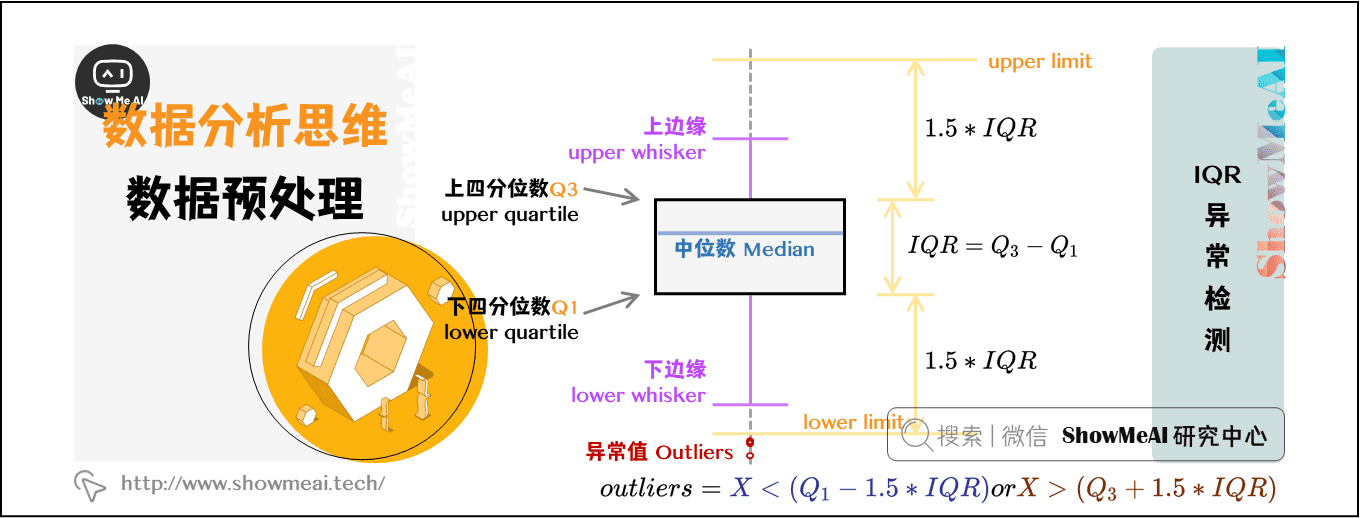
四分位数范围（Interquartile Range，简称IQR）是另一种衡量数据分布离散程度的方法，它描述了中间50%数据的范围。IQR计算公式如下：

[ IQR = Q3 - Q1 ]

其中，(Q3)是数据的第三四分位数（即上四分位数），(Q1)是数据的第一四分位数（即下四分位数）。IQR方法通过计算数据点与(Q1)和(Q3)的差距来识别异常值。通常，如果数据点小于(Q1 - 1.5 \times IQR)或大于(Q3 + 1.5 \times IQR)，则被认为是异常的。

4.2.2 IQR在异常检测中的应用

在异常检测中，使用IQR方法可以识别那些远离主体数据集的点。对于那些可能受到极端值影响的数据集，IQR方法特别有效，因为它不依赖于数据的正态分布假设。

下面是一个计算IQR值并识别异常点的Python代码示例：

def calculate_iqr(data):
    # 计算第一、第三四分位数
    Q1 = np.percentile(data, 25)
    Q3 = np.percentile(data, 75)
    IQR = Q3 - Q1
    # 确定异常值范围
    lower_bound = Q1 - 1.5 * IQR
    upper_bound = Q3 + 1.5 * IQR
    return IQR, lower_bound, upper_bound

# 示例数据
data = np.array([1, 2, 3, 4, 5, 100])

# 计算IQR及异常值范围
IQR, lower_bound, upper_bound = calculate_iqr(data)
print("IQR:", IQR)
print("Lower Bound:", lower_bound)
print("Upper Bound:", upper_bound)

上述代码中，我们使用 numpy 库中的 percentile 函数计算第一和第三四分位数，然后计算IQR值，并确定了异常值的下界和上界。

4.3 Z-score与IQR方法比较

4.3.1 适用场景对比

Z-score方法和IQR方法各有其适用场景。Z-score更适合于数据点服从或近似服从正态分布的情况，因为它是基于标准差的概念。而IQR方法则不受数据分布的限制，尤其适用于偏斜分布或包含离群点的数据集。

4.3.2 精确度和效率对比

在计算效率方面，IQR方法通常较快，因为它的计算主要依赖于四分位数，而Z-score方法依赖于整个数据集的平均值和标准差。精确度方面，两者都有可能因为异常值的存在而受到影响。Z-score方法在处理大量数据时可能受到异常值的影响较大，而IQR方法则相对稳健。

为了在实际应用中做出选择，我们需要根据数据集的特点和异常检测的目标来决定使用哪种方法。对于大型、多样化的数据集，可能需要结合多种方法来获得最佳的异常检测结果。

5. Ruby实现时间序列异常检测

5.1 Ruby中实现统计分析的步骤

在使用Ruby进行时间序列异常检测之前，我们需要经历一系列的统计分析步骤。这些步骤可以帮助我们更好地理解数据集，并识别出数据中的异常值。

5.1.1 数据收集与预处理

数据收集是任何分析工作的第一步。在Ruby中，你可以使用各种库，如 Net::HTTP 或 Typhoeus ，来从API或网页抓取数据。此外，使用CSV或JSON库可以将抓取的数据存储在文件中，并从这些文件中读取数据以进行分析。

一旦数据被加载到Ruby程序中，预处理就开始了。预处理的目的在于确保数据质量，以便后续分析可以正确进行。这通常包括去除重复数据、格式化数据、处理缺失值以及对异常值进行初步识别。

5.1.2 统计分析与异常判定

在数据预处理后，下一步是进行统计分析。Ruby可以利用数学库如 statsample 或 matrix 来计算数据集的统计特性，比如平均数、中位数、标准差等。统计分析的结果可以用于进一步的异常判定。

异常判定是通过比较数据点与统计特性（如均值和标准差）的关系来进行的。任何显著偏离这些统计特性的数据点都可能是异常值。接下来，我们会使用Z-score和IQR方法详细讲解如何识别这些异常值。

5.2 数据预处理的必要性

在深入讲解Ruby代码实现异常检测之前，我们必须明白数据预处理的重要性。

5.2.1 缺失值处理

在收集的数据集中，缺失值是一种常见的问题。Ruby中的 Array#compact 方法可以用来去除数组中的 nil 值。如果缺失值不多，可以考虑直接删除这些记录；如果缺失值较多，可能需要采用插值方法进行填补，如使用前一个值、后一个值或均值等方法。

5.2.2 异常值处理

异常值的处理可以通过简单地将其从数据集中移除来完成。在Ruby中，可以使用数组的 delete_if 方法结合条件语句来实现。但请记住，在删除任何数据点之前，要确保它们确实是异常值，而不是数据收集或录入过程中真正的变异。

5.3 Ruby代码实现异常检测示例

现在，我们将通过示例来展示如何使用Ruby进行时间序列数据的异常检测。

5.3.1 简单数据集的异常检测

假设我们有一个简单的时间序列数据集，我们想要检测这个数据集中的异常值。

require 'statsample'

# 假设数据集是整数数组
data = [10, 12, 13, 12, 11, 10, 15, 100]

# 使用Statsample计算Z-score
mean = data.mean
sd = data.standard_deviation

# 标记Z-score大于3或小于-3的异常值
anomalies = data.select { |d| (d - mean).abs > (3 * sd) }
puts "异常值: #{anomalies}"

5.3.2 复杂数据集的异常检测

对于更复杂的数据集，我们可能需要使用更复杂的统计分析技术。例如，使用 IQR 来识别异常值。

# 假设数据集是整数数组
data = [10, 12, 13, 12, 11, 10, 15, 100, 200, 300]

# 计算四分位数
q1 = data.percentile(25)
q3 = data.percentile(75)
iqr = q3 - q1

# 标记在1.5*IQR范围之外的异常值
lower_bound = q1 - 1.5 * iqr
upper_bound = q3 + 1.5 * iqr
anomalies = data.select { |d| d < lower_bound || d > upper_bound }
puts "异常值: #{anomalies}"

5.3.3 异常检测结果的评估与解释

最后，我们将对检测到的异常值进行评估和解释。例如，我们可能需要将检测到的异常值与数据收集的时间背景进行对比分析，来确定这些异常值是否是由外部因素导致的。

由于篇幅限制，我们不在此处展示复杂的评估与解释过程，但请记住，对异常值的解释是数据分析中的关键步骤，它要求分析人员具备业务知识以及对数据的理解。

本文还有配套的精品资源，点击获取

简介：时间序列数据分析是统计学的一个重要分支，尤其在大数据和机器学习中非常重要。本项目展示了如何使用Ruby编程语言检测时间序列数据中的异常值。时间序列数据是按时间顺序排列的一组数据点，如股票价格或网站访问量等，并可能展现趋势性、季节性和周期性特征。异常值可能由错误、异常情况或罕见事件引起，对分析结果影响重大。在本项目中，我们基于正态分布假设，采用Z-score和IQR方法来识别异常。开发者需要预处理数据，并可能调整方法以适应特定场景。

本文还有配套的精品资源，点击获取