1. Guide
More generally, consider a classification or regression problem where we would like to predict the value of some random variable y as a function of x. To derive a GLM for this problem, we will make the following three assumptions about the conditional distribution of y given x and about our model:
a. y | x; θ ∼ ExponentialFamily(η). I.e., given x and θ, the distribution of y follows some exponential family distribution, with parameter η.
b. Given x, our goal is to predict the expected value of T(y) given x. In most of our examples, we will have T(y) = y, so this means we would like the prediction h(x) output by our learned hypothesis h to satisfy hθ(x) = E[y|x]. (Note that this assumption is satisfied in the choices for h(x) for both logistic regression and linear regression. For instance, in logistic regression, we had hθ(x) = p(y = 1|x; θ) = 0 · p(y = 0|x; θ) + 1 · p(y = 1|x; θ) = E[y|x; θ].)
c. The natural parameter η and the inputs x are related linearly: η = θTx. (if η is vector-valued, then ηi = θiTx. θ=(θ1, θ2,...θk)T, θ1, θ2,...θk are all n+1-vectors, the target variable y will be k-vector)
---These three assumptions/design choices will allow us to derive a very elegant class of learning algorithms, namely GLMs, that have many desirable properties such as ease of learning.
2. Ordinary Least Squares
Consider the setting where the target variable y (also called the response variable in GLM terminology) is continuous, and we model the conditional distribution of y given x as as a Gaussian N(μ, σ2).
h(x) = E[y|x; θ]= μ = η = θT x.
3. Logistic Regression
Here we are interested in binary classification, so y ∈ {0, 1}. Given that y is binary-valued, it therefore seems natural to choose the Bernoulli family of distributions to model the conditional distribution of y given x.
h(x) = E[y|x; θ]= φ = 1/(1 + e−η) = 1/(1 + e−θT x)
You are previously wondering how we came up with the form of the logistic function 1/(1 + e−z), this gives one answer: Once we assume that y conditioned on x is Bernoulli, it arises as a consequence of the definition of GLMs and exponential family distributions.
Note: To introduce a little more terminology, the function g giving the distribution’s mean as a function of the natural parameter (g(η) = E[T(y); η]) is called the canonical response function. Its inverse, g−1, is called the canonical link function. Thus, the canonical response function for the Gaussian family is just the identify function; and the canonical response function for the Bernoulli is the logistic function.
4. Softmax Regression
Consider a classification problem in which the response variable y can take on any one of k values, so y ∈ {1 2, . . . , k}.
To parameterize a multinomial over k possible outcomes, one could use k - 1parameters φ1, . . . , φk-1 specifying the probability of each of the outcomes.
For notational convenience, we will let φk = 1 − φ1 − φ2 − ... − φk-1, but we should keep in mind that this is not a parameter, and that it is fully specified by φ1, . . . , φk−1.
To express the multinomial as an exponential family distribution, we will define T(y) ∈ Rk−1 as follows:
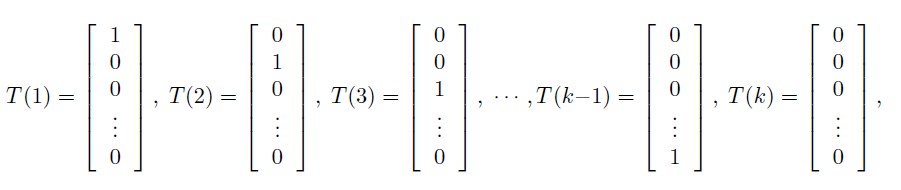
T(y) is now a k − 1 dimensional vector, rather than a real number. We will write (T(y))i to denote the i-th element of the vector T(y).
We introduce one more very useful piece of notation. An indicator function 1{·} takes on a value of 1 if its argument is true, and 0 otherwise. For example, 1{2 = 3} = 0, and 1{3 = 5 − 2} = 1.So, we can also write the relationship between T(y) and y as (T(y))i = 1{y = i}.
We have that E[(T(y))i] = P(y = i) = φi.
We are now ready to show that the multinomial is a member of the exponential family. We have:
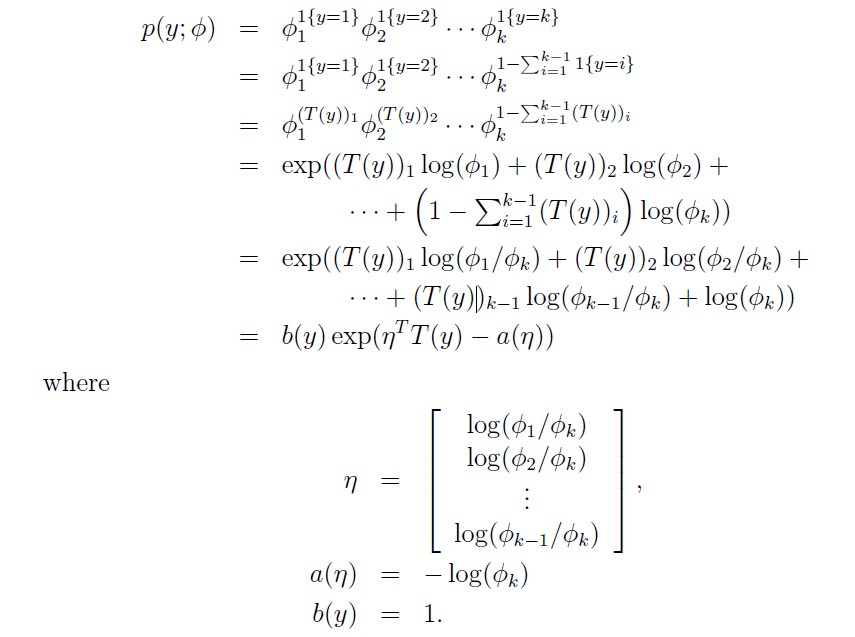
This completes our formulation of the multinomial as an exponential family distribution.
The link function is given (for i = 1, . . . , k) by
ηi = log(φi/φk)
For convenience, we have also defined ηk = log(φk/φk) = 0.
To invert the link function and derive the response function, we therefore have that:
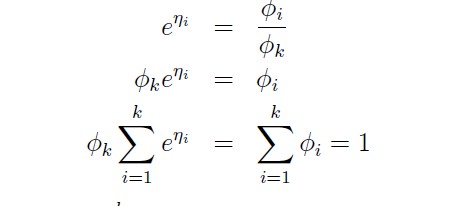
This will be:
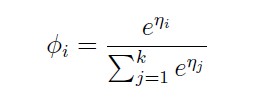
To complete our model, we use Assumption 3, given earlier, that the ηi’s are linearly related to the x’s. So, have ηi = θiTx (for i = 1, . . . , k − 1), where θ1, . . . , θk−1 ∈ Rn+1 are the parameters of our model. For notational convenience, we can also define θk = 0, so that ηk = θkTx = 0, as given previously. Hence, our model assumes that the conditional distribution of y given x is given by
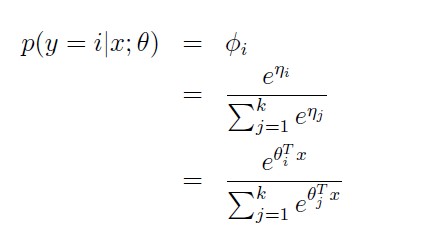
This model, which applies to classification problems where y ∈ {1, . . . , k}, is called softmax regression. It is a generalization of logistic regression.
Our hypothesis will output:
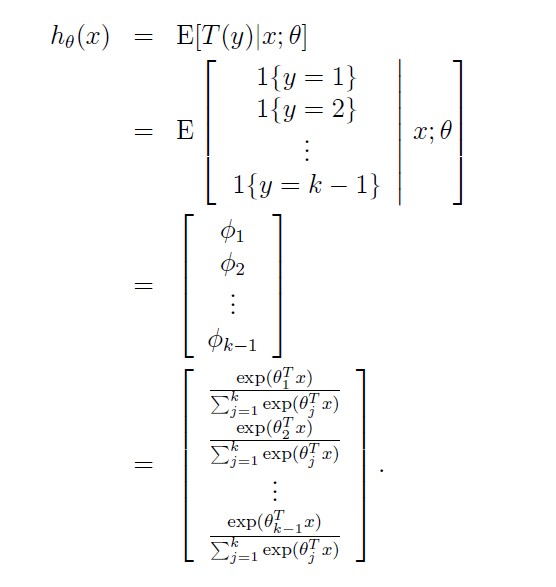
In other words, our hypothesis will output the estimated probability that p(y = i|x; θ), for every value of i = 1, . . . , k. (Even though hθ(x) as defined above is only k − 1 dimensional, clearly p(y = k|x; θ) can be obtained as 1 − φ1 − φ2 − ... − φk-1)
Lastly, lets discuss parameter fitting. Similar to our original derivation of ordinary least squares and logistic regression, if we have a training set of m examples {(x(i), y(i)); i = 1, . . . ,m} and would like to learn the parameters θi of this model, we would begin by writing down the log-likelihood:
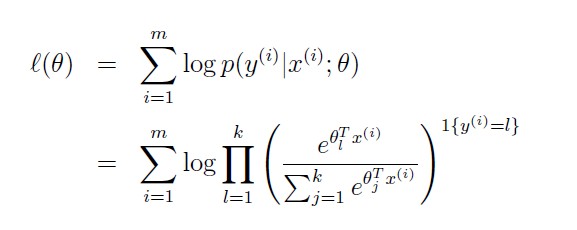
We can now obtain the maximum likelihood estimate of the parameters by maximizing l(θ) in terms of θ, using a method such as gradient ascent or Newton’s method.Here, θ is θ1,θ2,...,θk-1 are all n+1-vector.
Note: We can obtain for all GLM Models update rule like:
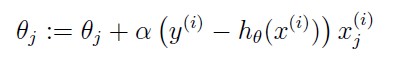




 本文介绍了广义线性模型(GLM)的基本概念,包括普通最小二乘法、逻辑回归及softmax回归,并探讨了如何通过最大似然估计来拟合模型参数。
本文介绍了广义线性模型(GLM)的基本概念,包括普通最小二乘法、逻辑回归及softmax回归,并探讨了如何通过最大似然估计来拟合模型参数。
















 1310
1310

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








