概述:
余弦相似度 是对两个向量相似度的描述,表现为两个向量的夹角的余弦值。当方向相同时(调度为0),余弦值为1,标识强相关;当相互垂直时(在线性代数里,两个维度垂直意味着他们相互独立),余弦值为0,标识他们无关。
Cosine similarity
is a measure of similarity between two vectors of an
inner product space
that measures the
cosine
of the angle between them. The cosine of 0° is 1, and it is less than 1 for any other angle. It is thus a judgement of orientation and not magnitude: two vectors with the same orientation have a Cosine similarity of 1, two vectors at 90° have a similarity of 0, and two vectors diametrically opposed have a similarity of -1, independent of their magnitude. Cosine similarity is particularly used in positive space, where the outcome is neatly bounded in [0,1].
定义
基础知识。。
The cosine of two vectors can be derived by using the Euclidean dot product formula:
Given two vectors of attributes, A and B, the cosine similarity, cos(θ), is represented using a dot product and magnitude as
The resulting similarity ranges from −1 meaning exactly opposite, to 1 meaning exactly the same, with 0 usually indicating independence, and in-between values indicating intermediate similarity or dissimilarity.
与皮尔森相关系数的关系
If the attribute vectors are normalized by subtracting the vector means (e.g.,
 ), the measure is called centered cosine similarity and is equivalent to the
Pearson Correlation Coefficient
.
), the measure is called centered cosine similarity and is equivalent to the
Pearson Correlation Coefficient
.
 ), the measure is called centered cosine similarity and is equivalent to the
Pearson Correlation Coefficient
.
), the measure is called centered cosine similarity and is equivalent to the
Pearson Correlation Coefficient
.




 本文介绍了余弦相似度的概念及其在正空间中的应用。余弦相似度通过计算两个向量之间的夹角余弦值来衡量它们的相关性。当向量完全相同或相反时,相似度分别为1或-1,而相互垂直时相似度为0。文中还探讨了余弦相似度与皮尔森相关系数之间的关系。
本文介绍了余弦相似度的概念及其在正空间中的应用。余弦相似度通过计算两个向量之间的夹角余弦值来衡量它们的相关性。当向量完全相同或相反时,相似度分别为1或-1,而相互垂直时相似度为0。文中还探讨了余弦相似度与皮尔森相关系数之间的关系。
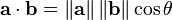
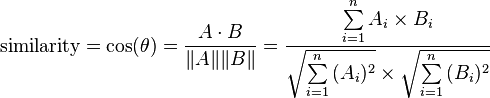
















 6745
6745

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








