201812-4 数据中心（kruskal）

最新推荐文章于 2026-01-06 12:00:34 发布

转载最新推荐文章于 2026-01-06 12:00:34 发布 · 118 阅读

0 ·

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/mlblog27/p/10544429.html

文章标签：

#java #数据结构与算法

考场上的时候被题目完全蒙住了，当时状态也不好，前几次考试每次考试当天就头晕感冒流鼻涕

好的，以上都是借口，自己没有好好复习才是真的...

题目：

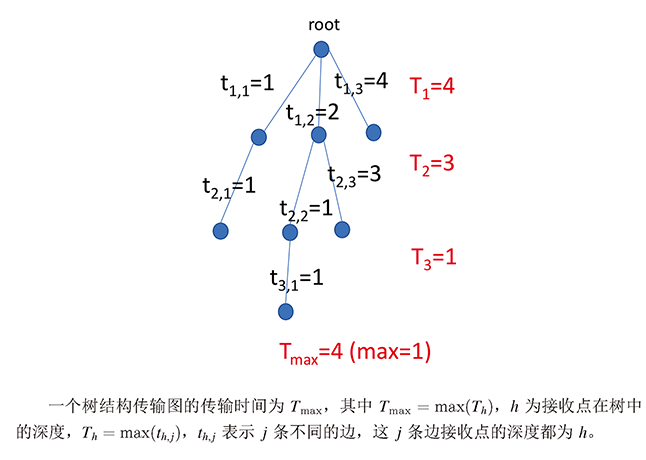
好的，以上题目简述就是：给你一个无向连通图，求它的最小生成树的最大边，姐妹们，如果你们考场看懂了题目带了数据结构书或者会krukal又怎么不会得分呢？

我就是没看懂题目得人啊！不过，通过我今天的验证，发现就算我看懂了题目我也不一定得分，因为我运行错误orz...

就是简单的使用了一下kruskal,整个算法清晰易懂

 1 #include<cstdio>
 2 #include<cstdlib>
 3 #include<algorithm>
 4 #include<iostream>
 5 using namespace std;
 6 //第一次提交：运行错误，查看代码，没啥问题啊？？？
 7 //第二次提交：修改MAX_VEX = 10^5, 改为5 * 1e5 + 10 ，记住乘方的表示方法 
 8 //...
 9 //第八次提交，100分，修改seek函数，由原来的while循环变为条件递归调用！！！然后在找到输出key的地方由原来条件判断来查找i，变成了最后直接计算查找i
10 //姐妹们，要记住当整个测试数据很大的时候，即使你的计算即使if,但是放到while里面，该大的数据还是大，我们尽量一点点抠时间总能给你节约出来 
11 const int MAX_VEX = 5*1e5 + 10;
12 int set[MAX_VEX];
13 typedef struct edged{
14     int bv, ev, w;
15 }Edges;
16 Edges edgeset[2 * MAX_VEX];
17 
18 bool cmp(Edges a,Edges b){
19     return a.w < b.w;
20 } 
21 
22 int seeks(int v){
23     return set[v] == v ? v : set[v] = seeks(set[v]);
24 }
25 
26 int kruskal(int n, int m){
27     int v1, v2, i;
28     for(i = 1; i <= m; i++){
29         set[i] = i;
30     }
31     int u = 0;//u记录连接的边的数量，当u = n-1时，已经构造处一棵树 
32     int key;
33     i = 0;
34     while(u < n-1){
35         v1 = seeks(edgeset[i].bv);//确定边的顶点所在连通分量的根节点
36         v2 = seeks(edgeset[i].ev);
37         if(v1 != v2){
38             set[v1] = v2;
39             u += 1;
40         }
41         i++;
42     }
43     i = i-1;
44     key = edgeset[i].w;
45     return key;
46 }
47 
48 int main(){
49     int n, m, root;
50     cin >> n >> m >> root;
51     for(int i = 1; i <= m; i++){
52         cin >> edgeset[i].bv >> edgeset[i].ev >> edgeset[i].w;
53     }
54     sort(edgeset+1,edgeset+m+1,cmp);//对边集数组按权值升序排序，其中n为元素个数，即图的边数 
55     int t = kruskal(n, m);
56     cout << t;
57     return 0;
58 }