[Luogu 3902]Increasing

最新推荐文章于 2025-03-04 22:58:40 发布

转载最新推荐文章于 2025-03-04 22:58:40 发布 · 46 阅读

0 ·

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/Y-E-T-I/p/7636659.html

本文介绍了一种求解最长不下降子序列的算法，并通过具体示例代码讲解了如何利用离散化与线段树的方法实现该算法。适用于解决特定类型的问题，如填充整数序列。

Description

Input

Output

Sample Input

3
1 3 2

Sample Output

HINT

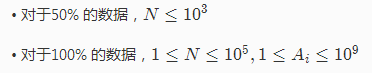
这里要用到一种技巧：

我们认为改出来的数要是整数情况下：

a[i]>a[i-1]等价于a[i]-i>=a[i-1]-i+1

这样求最长不下降子序列就行了

因为当j<i a[j]-j==a[i]-i时，说明他们中间可以填的数有i-j+1个，需要的正好也是i-j+1

所以这样是肯定可以的

如果不处理就求最长上升子序列，可能会出现中间部分无数可以填入(所以只适用于填实数)

nlogn求最长不下降有很多方法，这里用的是离散+线段树

 1 #include<iostream>
 2 #include<cstdio>
 3 #include<cstring>
 4 #include<algorithm>
 5 using namespace std;
 6 int c[400001],sz;
 7 int a[100001],b[100001],n,ans,f[100001];
 8 void pushup(int rt)
 9 {
10   c[rt]=max(c[rt*2],c[rt*2+1]);
11 }
12 void update(int rt,int l,int r,int x,int d)
13 {
14   if (l==r)
15     {
16       c[rt]=d;
17       return;
18     }
19   int mid=(l+r)/2;
20   if (x<=mid) update(rt*2,l,mid,x,d);
21   else update(rt*2+1,mid+1,r,x,d);
22   pushup(rt);
23 }
24 int query(int rt,int l,int r,int L,int R)
25 {
26   if (l>=L&&r<=R)
27     {
28       return c[rt];
29     }
30   int mid=(l+r)/2,s=0;
31   if (L<=mid) s=max(s,query(rt*2,l,mid,L,R));
32   if (R>mid) s=max(s,query(rt*2+1,mid+1,r,L,R));
33   return s;
34 }
35 int main()
36 {int i,num=0;
37   cin>>n;
38   for (i=1;i<=n;i++)
39     {
40       scanf("%d",&a[i]);
41       num++;
42       b[num]=a[i]-i;
43       a[i]-=i;
44     }
45   sort(b+1,b+num+1);
46   sz=unique(b+1,b+num+1)-(b+1);
47   for (i=1;i<=n;i++)
48     a[i]=lower_bound(b+1,b+sz+1,a[i])-b;
49   for (i=1;i<=n;i++)
50     {
51       f[i]=query(1,1,sz,1,a[i])+1;
52       update(1,1,sz,a[i],f[i]);
53       ans=max(ans,f[i]);
54     }
55   cout<<n-ans;
56 }