参考博客链接:https://www.cnblogs.com/yjiyjige/p/3263858.html
本文仅仅基于上文谈谈自己的心得,以便更好大家理解,也便于自己理解。如有错误,欢迎指正。Thanks♪(・ω・)ノ
emmmm........更多详情请参考原博客。
接着我们来看:
作者于开头提出:
1.什么是KMP算法以及它的来历;
2.一般的解决 匹配模式串 问题的思路;

基于这个想法我们可以得到以下的程序:
1 /** 2 3 * 暴力破解法 4 5 * @param ts 主串 6 7 * @param ps 模式串 8 9 * @return 如果找到,返回在主串中第一个字符出现的下标,否则为-1 10 11 */ 12 13 public static int bf(String ts, String ps) { 14 15 char[] t = ts.toCharArray(); 16 17 char[] p = ps.toCharArray(); 18 19 int i = 0; // 主串的位置 20 21 int j = 0; // 模式串的位置 22 23 while (i < t.length && j < p.length) { 24 25 if (t[i] == p[j]) { // 当两个字符相同,就比较下一个 26 27 i++; 28 29 j++; 30 31 } else { 32 33 i = i - j + 1; // 一旦不匹配,i后退 34 35 j = 0; // j归0 36 37 } 38 39 } 40 41 if (j == p.length) { 42 43 return i - j; 44 45 } else { 46 47 return -1; 48 49 } 50 51 }
这是对应 一般的解决 匹配模式串 问题的思路 的代码。
接着作者提出一些 用此一般方法解决一些问题会比较麻烦并提出要人为地有记忆性地查找 正如作者说:
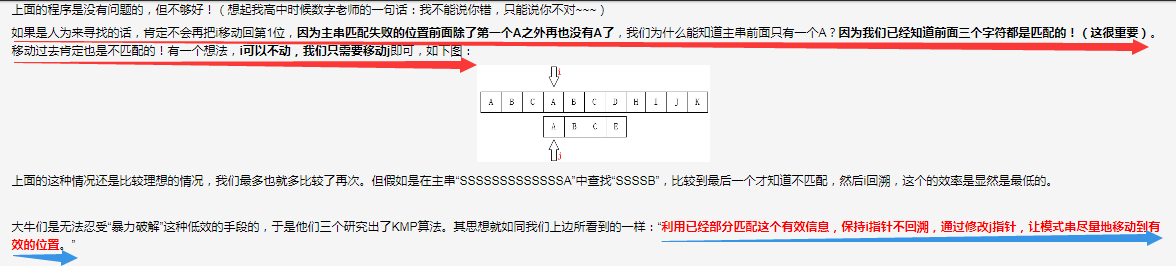
而保持i指针不回溯,可以省时省力,更简单有效解决问题。
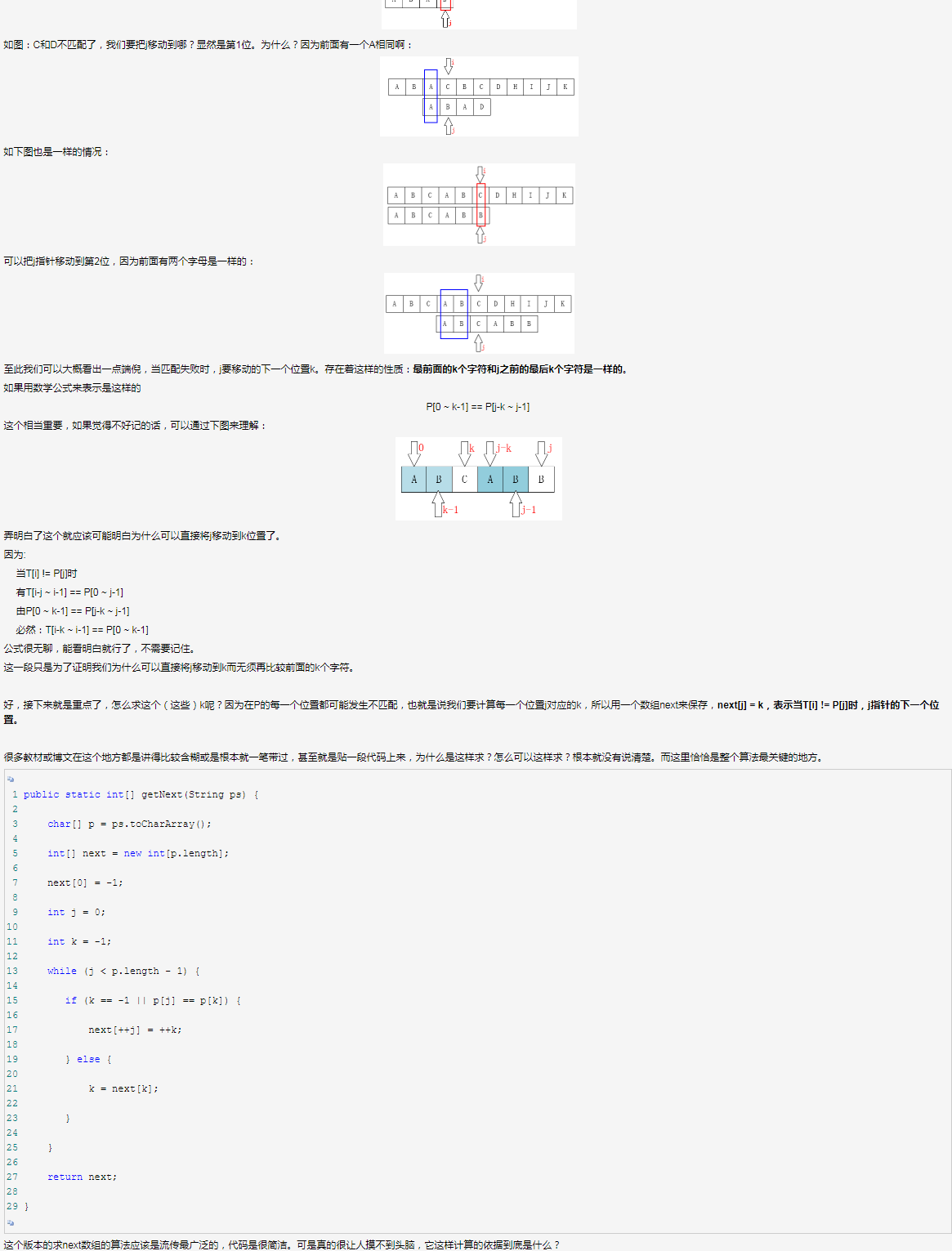

关于这个k=next[k]的依据,不理解的朋友不妨拿一个模式串循环一遍,比如ABACB......
他的作用就是加入你在进行 主串与模式串 比较匹配过程中,假如前面已经有了一段已经匹配的串,那么当你遇到当前的j指针指向的字母与i指针指向字母不匹配,那可以利用自身前面已匹配的部分,进行j的回溯,假如还是不匹配,再利用前面已经匹配的部分(尽管它现在越来越短),进行j的回溯.......(如此反复进行下去,进行多次有效的利用)。这个过程就类似于一直进行自身的(逐渐变短的)前缀和自身的后缀进行匹配。
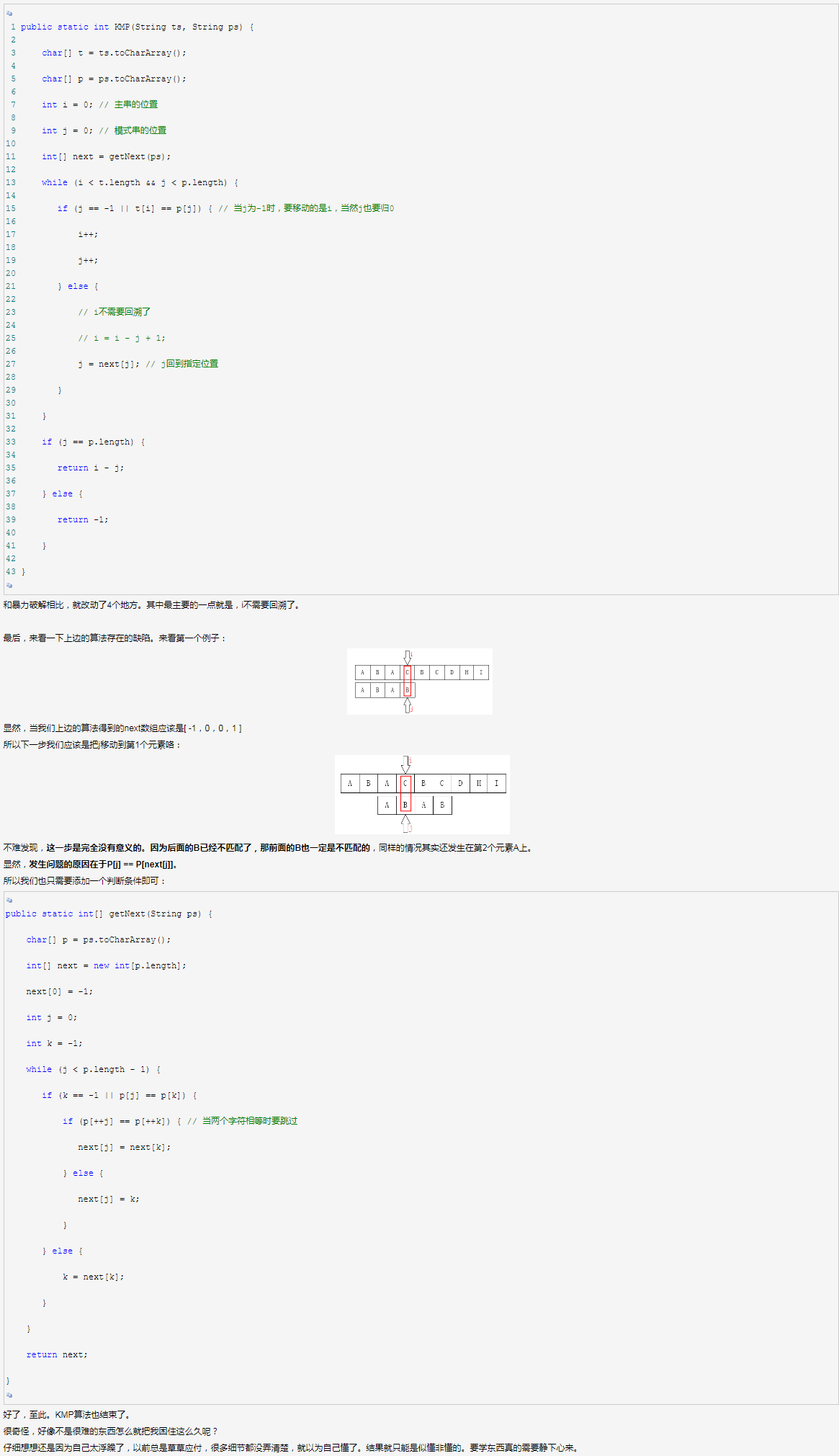
先得到next数组
再进行主串与模式串的匹配
作者写的很到位
over!




















 4169
4169

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








