HDU 5810 Balls and Boxes(盒子与球)
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Others)
|
Description |
题目描述 |
|
Mr. Chopsticks is interested in random phenomena, and he conducts an experiment to study randomness. In the experiment, he throws n balls into m boxes in such a manner that each ball has equal probability of going to each boxes. After the experiment, he calculated the statistical variance V as Your task is to find out the expected value of V. |
Chopsticks先生突然对随机现象来了兴趣,还做了个实验来研究随机性。实验中,他将n个球等概率丢进m个盒子里。然后,他用下面的式子计算方差V
你的任务就是找出V的期望。 |
|
Input |
输入 |
|
The input contains multiple test cases. Each case contains two integers n and m (1 <= n, m <= 1000 000 000) in a line. The input is terminated by n = m = 0. |
多组测试用例。每个测试用例有一行两个整数n和m(1 <= n, m <= 1000 000 000)。 n = m = 0 时,输入结束。
|
|
Output |
输出 |
|
For each case, output the result as A/B in a line, where A/B should be an irreducible fraction. Let B=1 if the result is an integer.
|
对于每个用例,输出一行结果A/B,A/B为不可约分数。结果为整数时,令B=1。
|
|
Sample Input - 输入样例 |
Sample Output - 输出样例 |
|
2 1 |
0/1 |
|
Hint |
提示 |
|
In the second sample, there are four possible outcomes, two outcomes with V = 0 and two outcomes with V = 1.
|
在第二个样例中,有4种可能结果,两种V = 0和一种V = 1。 |
【题解】
类似二项分布的实验,得到所有可能的方差,再对方差取期望……等等,这不就是求二项分布的方差吗?(脑子一抽:所有可能 + 取期望 = 等概率)
二项分布D(X) = np(1-p)
p = 1/m 带入D(X) 得 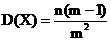
【代码 C++】
1 #include <cstdio> 2 __int64 GCD(__int64 a, __int64 b){ 3 __int64 c; 4 while (c = a%b) a = b, b = c; 5 return b; 6 } 7 int main(){ 8 __int64 n, m, g; 9 while (scanf("%I64d%I64d", &n, &m), n + m){ 10 n *= m - 1; m *= m; 11 g = GCD(n, m); 12 printf("%I64d/%I64d\n", n / g, m / g); 13 } 14 return 0; 15 }







 本文介绍了HDU 5810 Balls and Boxes的题目背景及解决方法,通过理解实验中球等概率分配到盒子的过程,采用二项分布原理求解方差的期望值。
本文介绍了HDU 5810 Balls and Boxes的题目背景及解决方法,通过理解实验中球等概率分配到盒子的过程,采用二项分布原理求解方差的期望值。
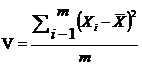 Where
Where 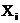 is the number of balls in the ith box, and
is the number of balls in the ith box, and 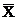 is the average number of balls in a box.
is the average number of balls in a box.















 603
603

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








