hdu4767_Bell_矩阵快速幂+中国剩余定理-优快云博客

本文深入探讨了贝尔数的计算方法，通过矩阵快速幂和中国剩余定理解决了贝尔数求解过程中的复杂问题。详细介绍了贝尔数的基本概念、维基百科中的相关公式及实例应用。

2013长春赛区网络赛的1009题

比赛的时候这道题英勇的挂掉了，原因是写错了一个系数，有时候粗心比脑残更可怕

本题是关于Bell数，关于Bell数的详情请见维基：http://en.wikipedia.org/wiki/Bell_number

其中有一句话是这么说的： And they satisfy "Touchard's congruence": If p is any prime bumber then

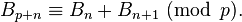
$B_{p+n}\equiv B_n+B_{n+1}\ (\operatorname{mod}\ p).$

但95041567不是素数，分解之后发现 95041567 = 31 × 37 × 41 × 43 × 47

按照上述递推式，利用矩阵快速幂可以得到 B_nmod p, (p = 31, 37, 41, 43, 47)，因为p最大47,所以矩阵快速幂O(p^3 * log(n/p))不会超时，

当然要先利用以下公式把B1-B47预处理出来：

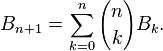
$B_{n+1}=\sum_{k=0}^{n}{{n \choose k}B_k}.$

得到5个B_nmod p (p = 31, 37, 41, 43, 47)之后，怎样得到B_nmod Πp 呢？

利用中国剩余定理可以完美的解决上述问题

详情见代码：

#include <cstdio>
#include <cstring>

#define MOD 95041567
#define LL long long

const int maxn = 50; //必须加 const，否则编译错误
LL x[5] = {31, 37, 41, 43, 47};
LL X;

class Matrix {
public:
    LL val[maxn][maxn];
    Matrix() {
        memset(val, 0, sizeof(val));
    }

    Matrix operator*(const Matrix& c) const {
        Matrix res;
        for (int i = 0; i < X; ++i)
            for (int j = 0; j < X; ++j)
                for (int k = 0; k < X; ++k) {
                    res.val[i][j] += val[i][k] * c.val[k][j];
                    res.val[i][j] = (res.val[i][j] + X) % X; //防止矩阵元素变为负数，若不需要，去掉"+MOD"
                }
        return res;
    }

    Matrix operator*=(const Matrix& c) {
        *this = *this * c;
        return *this;
    }

    Matrix Pow(LL k) { //返回one^k
        Matrix res = Zero();
        Matrix step = One();
        while (k) {
            if (k & 1)
                res *= step;
            k >>= 1;
            step *= step;
        }
        return res;
    }

    Matrix Zero() const {
        Matrix res;
        for (int i = 0; i < X; ++i)
            res.val[i][i] = 1;
        return res;
    }

    Matrix One() const {
        Matrix res;
        for (int i = 0; i < X - 1; ++i)
            res.val[i][i] = res.val[i + 1][i] = 1;
        res.val[0][X - 1] = res.val[1][X - 1] = res.val[X - 1][X - 1] = 1;
        return res;
    }
};

void gcd(LL a, LL b, LL& d, LL& xx, LL& y) {
    if (!b) {
        d = a, xx = 1, y = 0;
    } else {
        gcd(b, a % b, d, y, xx);
        y -= xx * (a / b);
    }
}

LL china(LL n, LL* a, LL* m) {
    LL M = 1, d, xx = 0, y;
    for (int i = 0; i < n; ++i) M *= m[i];
    for (int i = 0; i < n; ++i) {
        LL w = M / m[i];
        gcd(m[i], w, d, d, y);
        xx = (xx + y * w * a[i]) % M;
    }
    return (xx + M) % M;
}

LL c[50][50], f[50], a[5];

int main() {
    int T;
    for (int i = 0; i < 50; ++i) {
        c[i][0] = c[i][i] = 1;
        for (int j = 1; j < i; ++j)
            c[i][j] = (c[i-1][j] + c[i - 1][j - 1]) % MOD;
    }
    f[0] = 1;
    f[1] = 1;
    for (int i = 2; i < 50; ++i) {
        for (int j = 0; j < i; ++j)
            f[i] = (f[i] + c[i - 1][j] * f[j]) % MOD;
    }
    scanf("%d", &T);
    while (T--) {
        LL n;
        scanf("%I64d", &n);
        if (n < 50) {
            printf("%I64d\n", f[n]);
            continue;
        }
        memset(a, 0 ,sizeof(a));
        for (int i = 0; i < 5; ++i) {
            X = x[i];
            Matrix m;
            m = m.Pow(n / X);
            for (int j = 0; j < X; ++j)
                a[i] = (a[i] + f[j] * m.val[j][n % X]) % X;
        }
        printf("%I64d\n", china(5, a, x));
    }
    return 0;
}

转载于:https://www.cnblogs.com/Chierush/p/3344661.html