算法之“冒泡排序”-2

冒泡排序：有两组数据，都是没有规矩的排序，现在将两组数据合并，并按照从小到大的数据排序：

百度百科解释：

基本概念　　冒泡排序（BubbleSort）的基本概念是：依次比较相邻的两个数，将小数放在前面，大数放在后面。即在第一趟：首先比较第1个和第2个数，将小数放前，大数放后。然后比较第2个数和第3个数，将小数放前，大数放后，如此继续，直至比较最后两个数，将小数放前，大数放后。至此第一趟结束，将最大的数放到了最后。在第二趟：仍从第一对数开始比较（因为可能由于第2个数和第3个数的交换，使得第1个数不再小于第2个数），将小数放前，大数放后，一直比较到倒数第二个数（倒数第一的位置上已经是最大的），第二趟结束，在倒数第二的位置上得到一个新的最大数（其实在整个数列中是第二大的数）。如此下去，重复以上过程，直至最终完成排序。

 

　　由于在排序过程中总是小数往前放，大数往后放，相当于气泡往上升，所以称作冒泡排序。

 

　　用二重循环实现，外循环变量设为i，内循环变量设为j。假如有10个数需要进行排序，则外循环重复9次，内循环依次重复9，8，...，1次。每次进行比较的两个元素都是与内循环j有关的，它们可以分别用a[j]和a[j+1]标识，i的值依次为1,2,...,9，对于每一个i,j的值依次为1,2,...10-i。

产生

　　在许多程序设计中，我们需要将一个数列进行排序，以方便统计，而冒泡排序一直由于其简洁的思想方法而倍受青睐。

排序过程

　　设想被排序的数组R[1..N]垂直竖立，将每个数据元素看作有重量的气泡，根据轻气泡不能在重气泡之下的原则，从下往上扫描数组R，凡扫描到违反本原则的轻气泡，就使其向上"漂浮"，如此反复进行，直至最后任何两个气泡都是轻者在上，重者在下为止。

 

编辑本段性能分析

　　若记录序列的初始状态为"正序"，则冒泡排序过程只需进行一趟排序，在排序过程中只需进行n-1次比较，且不移动记录；反之，若记录序列的初始状态为"逆序"，则需进行n(n-1）/2次比较和记录移动。因此冒泡排序总的时间复杂度为O(n*n)。

个人代码示例：

using System;
using System.Collections.Generic;
namespace Compare
{
    class Program
    {
        static void Main(string[] args)
        {
            int[] array1 = new int[] { 1, 15, 51, 35, 45, 15, 45 };
            int[] array2 = new int[] { 2, 15, 145, 26, 89, 5, 48 };
            List<int> list = new List<int>();
            list.AddRange(array1);
            List<int> list2 = new List<int>();
            list2.AddRange(array2);
            Console.WriteLine("数据1：");
            foreach (int d in list)
            {
                Console.Write(d + " ");
            }
            Console.WriteLine("\n数据2：");
            foreach (int d in list2)
            {
                Console.Write(d + " ");
            }
            Console.WriteLine("\n排序后：");
            foreach (int o in CompareList(list, list2))
            {
                Console.Write(o + " ");
            }
            Console.ReadKey();
        }
        public static List<int> CompareList(List<int> L1, List<int> L2)
        {
            int temp=0;
            //通过冒泡排序先各自对集合从小到大排序
            for (int k = 0; k < L1.Count - 1; k++)
            {
                for (int n = 0; n < L1.Count -k- 1; n++)
                {
                    if (L1[n] > L1[n + 1])
                    {
                        temp = L1[n];
                        L1[n] = L1[n + 1];
                        L1[n + 1] = temp;
                    }
                }
            }
            for (int k = 0; k < L2.Count - 1; k++)
            {
                for (int n = 0; n < L2.Count - k-1; n++)
                {
                    if (L2[n] > L2[n + 1])
                    {
                        temp = L2[n];
                        L2[n] = L2[n + 1];
                        L2[n + 1] = temp;
                    }
                }
            }
            //以下是两个集合进行比较
            List<int> TempList = new List<int>();
            int i = 0, j = 0;
            while ((i <= (L1.Count - 1) && (j <= (L2.Count - 1))))
            {
                if (L1[i] < L2[j])
                {
                    TempList.Add(L1[i++]);
                }
                else
                {
                    TempList.Add(L2[j++]);
                }

            }
            while (i <= (L1.Count - 1))
            {
                TempList.Add(L1[i++]);
            }

            while (j <= (L2.Count - 1))
            {
                TempList.Add(L2[j++]);
            }
            return TempList;
        }
    }
}

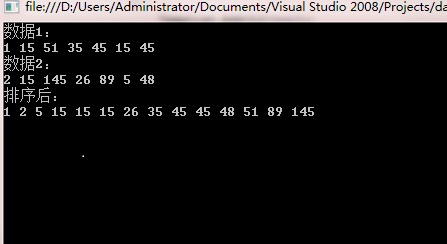
 运行结果：

转载于:https://www.cnblogs.com/zhangweijia/archive/2012/12/26/2833411.html