二维数组循环求出最大子数组-优快云博客

本文探讨了一种使用动态规划方法解决二维数组中最大子矩阵问题的算法，通过将二维数组转化为一维数组，实现了问题的高效解决。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

package shengcheng;

import java.util.Scanner;

import org.junit.Test;

public class ErweiXunhuan {

@Test
public void fun()
{
    int [][]a=new int[4][8];
    Scanner write=new Scanner(System.in);
    for(int i=0;i<4;i++)
    {
        for(int j=0;j<4;j++)
        {
            a[i][j]=write.nextInt();
            a[i][j+4]=a[i][j];
        }
    }
    
    int  max=-200000;
    int []sum=new int [8];
  
    int  add =-200000 ;
    for(int i=0;i<4;i++)
    {
        for(int l=0;l<8;l++)
        {
            sum[l]=0;
        }
        for(int j=i;j<4;j++)
        {
                           
            for(int k=0;k<8;k++)
            {
                sum[k]+=a[j][k];
            }
         
                add=DP(sum,4);
            }
        
        if(add>max)
        {
            max=add;
        }


    }
    System.out.println(max);
    
    
    
    
    
}

 public  int DP(int  a[],int n)
 {
   
     int  Max=a[0];
     int temp=-200000;
     for(int i=0;i<n;i++)
        {
           temp=-200000;
           for(int j=i;j<n+i;j++)
           {
            
             temp+=a[j];
             if(temp>Max)
             {
                 Max=temp;
             }
             
             if(temp<0)
             {
                 temp=a[j];
             }
            
           }
        }
     return Max; 
      }
    
    
    
}

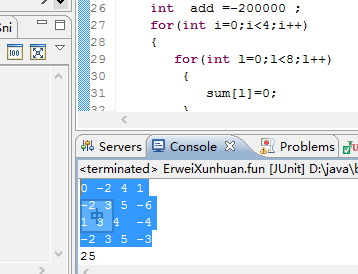
　　老师出了这道题目的时候，我首先联想到原来的一维数组循环求最大子矩阵，然后还想到原来的二维数组求最大子矩阵，感觉可以利用原来的思路继续思考下去，于是我就想原来的二维数组的求最大的子矩阵也是将二维转化为一维的，然后再将一维的数组进行动态规划，这样就解决原来二维的问题，于是我就用相同的方法将二维的的列数扩大一倍这样就起到循环的目的，然后将这个二维数组再转化为一维数组，然后这样就能利用上原来的一维循环数组就这样可以解决了问题。

转载于:https://www.cnblogs.com/qerror404/p/4450893.html