总体框架

Time Value
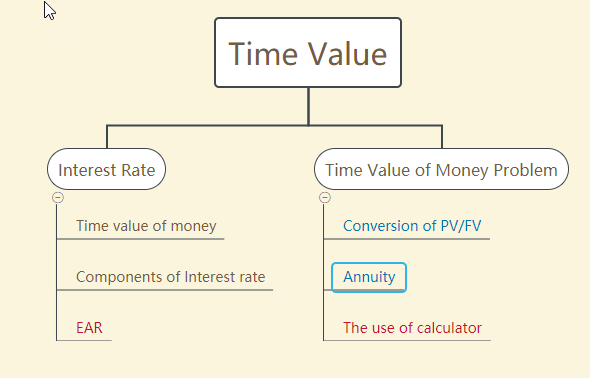
Interest Rate
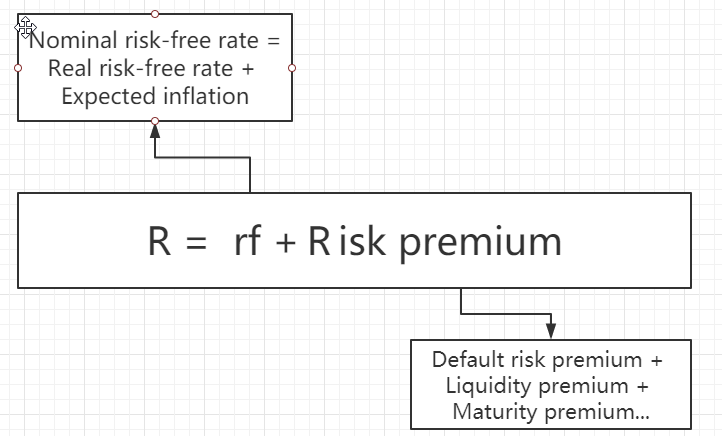
rf: 无风险收益率 (CFA中一般认为是美国短期国债T-bill的收益率)
Nominal risk-free rate: 名义无风险税率
Real risk-free rate: 实际无风险利率
Liquidity premium: 流动性风险溢价
Maturity premium: 到期风险溢价
Risk premium: 风险溢价
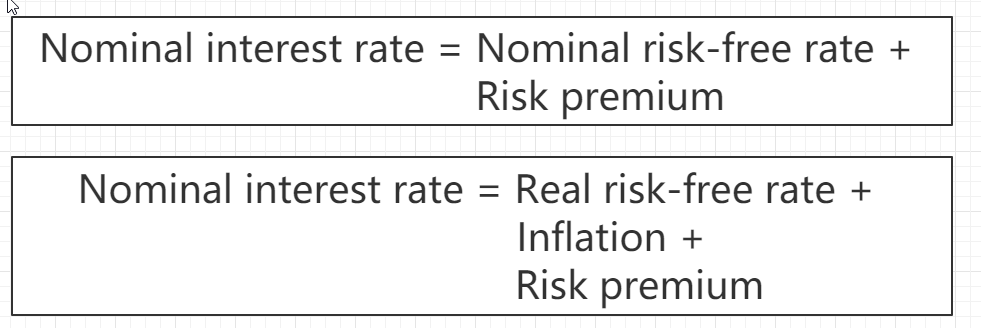
费雪效应
Nominal interest rate和Stated Interest rate是一个概念
Effective annual rate(EAR)
For discrete compounding
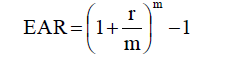
- Where: m is the compounding frequency
- r is the noinal/quoted/stated annual interest rate
- r/m is periodic interest rate
For continuous compounding
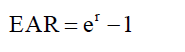
- 时时刻刻分分秒秒在计息.
- 例: 算名义年利率是8%, 求连续计算情形下的EAR.
- 计算器按法: 0.08 --> 2ND --> LN ==>结果: 1.083287
Conversion of PV/FV
Present Value (PV)
- The value of an initial investment.
Future Value (FV)
- The value of an initial investment would be worth n period from today.
Conversion of PV/FV:
- compounding:
-
- continuous compounding:
-
- 站在今天去推测未来会价值几何: PV --> FV : 复利
- 站在未来推测今天需要存入多少: FV --> PV :折现
Annuity
Ordinary annuity
- all constant cash flows occuring at the end of each period(END), 后付年金
Annuity due
- all constant cash flows occuring at the beginning of each period(BEG), 先付年金

Prepetuity
- a set of constant never-ending sequential cash flows occuring at the end of each period, 永续年金
- PV = A/R
- where A: the periodic payment
- r: the periodic return
- PV = A/R

推荐用第三种方式, 就不用再把计算器在END和BGN模式之间去转换.




 本文介绍了金融数学中的关键概念,包括无风险收益率、名义利率、实际利率等,并解释了有效年利率的计算方法及其与名义利率的区别。同时,文章还讨论了现值与终值的转换方法及年金和永续年金的概念。
本文介绍了金融数学中的关键概念,包括无风险收益率、名义利率、实际利率等,并解释了有效年利率的计算方法及其与名义利率的区别。同时,文章还讨论了现值与终值的转换方法及年金和永续年金的概念。
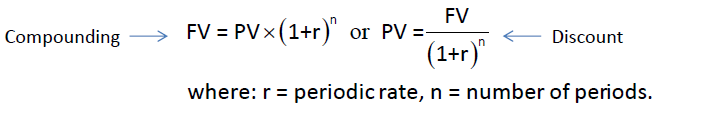
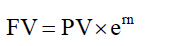

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








