BestCoder21 1002.Formula 解题报告-优快云博客

本文解析了HDU 5139题目的求解方法，介绍了如何通过离线处理避免内存溢出的问题，并给出了两种实现代码示例。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=5139

题目意思：给出一个数 n，求出 f(n)。

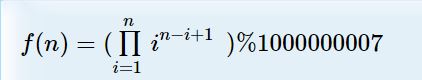
　　可以发现有以下规律：

　　f(1) = 1!

　　f(2) = 1! * 2!

　　f(3) = 1! * 2! * 3!

　　f(n) = 1! * 2! * 3! *....... * (n-1)! * n!

　　我一开始对题解中的直接打表超内存不太理解，于是就实践了下：

　　超内存版本（就是直接算 f[n]，当输入n的时候，输出 f[n]）：

（原来开大小为 1e7 的数组会这样滴，长见识了~~）

 1 #include <iostream>
 2 #include <cstdio>
 3 #include <cstring>
 4 #include <algorithm>
 5 using namespace std;
 6 
 7 const int MOD = 1e9 + 7;
 8 const int maxn = 1e7 + 2;
 9 
10 int f[maxn];
11 
12 int main()
13 {
14     int p = 1, s = 1;
15     for (int i = 1, j = 1; i <= maxn; i++)
16     {
17         while (j <= i)
18         {
19             p = 1ll * p * j % MOD;
20             s = 1ll * s * p % MOD;
21             j++;
22         }
23         f[i] = s;
24     }
25     int n;
26     while (scanf("%d", &n) != EOF)
27         printf("%d\n", f[n]);
28     return 0;
29 }

View Code

　　所以就要离线处理了，这位大哥讲得比较好。

http://blog.youkuaiyun.com/sr_19930829/article/details/41785767

　　即：对数据统一输入，统一处理，最后统一输出。

而为了防止超内存，开 1e5 大小的数组保存答案就可以了，因为题目中说了 cases 大约为100000。

　　输入完之后就要从小到大排序了，这样的好处能保证每个阶乘只计算一遍。而为了对应输入的顺序，需要 pair 数组的second 来保存序号。

 1 #include <iostream>
 2 #include <cstdio>
 3 #include <cstring>
 4 #include <algorithm>
 5 using namespace std;
 6 
 7 const int MOD = 1e9 + 7;
 8 const int maxn = 1e5 + 2;
 9 
10 pair<int, int> pii[maxn];
11 int ans[maxn];
12 
13 int main()
14 {
15     int cnt = 0;
16     while (scanf("%d", &pii[cnt].first) != EOF)
17     {
18         pii[cnt].second = cnt;
19         cnt++;
20     }
21 
22     sort(pii, pii+cnt);
23     int p = 1, s = 1;
24     for (int i = 0, j = 1; i < cnt; i++)
25     {
26         while (j <= pii[i].first)
27         {
28             p = 1ll * p * j % MOD;
29             s = 1ll * s * p % MOD;
30             j++;
31         }
32         ans[pii[i].second] = s;
33     }
34     for (int i = 0; i < cnt; i++)
35         printf("%d\n", ans[i]);
36     return 0;
37 }