机器学习（第五章）

神经元模型

最普遍的定义是：神经网络是由具有适应性的简单单元组成的广泛并行互联的网络，它的组织能够模拟生物神经系统对真实世界物体做出的交互反应。

神经网络的最基本成分是神经元模型。在生物网络中，神经元的活动是以0或1的状态存在的，一个神经元可以接受多个神经元的信号输入，当所有输入超出阈值时，接受输入的神经元就会发放（兴奋起来），然后向其他的神经元发送信号。只要没有超出阈值，不管输入的量有多大，该神经元都不会兴奋、并向其他神经元发送信号。（神经元的输入既可以是兴奋性的也可以是抑制性的）

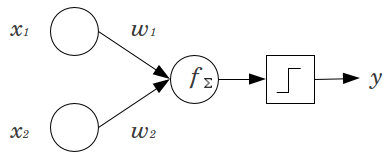
下图即是在1943年提出的最简化的抽象模型，

\[y=f(\sum_{i=1}^n{w_i}{x_i}-\theta)\]

每个输入和他们的权重的乘积的和，再减去阈值theta，就是该接受输入的神经元的输出了，这个输出要么为0，要么为1.激活函数（activation function）就是将输入和阈值进行比较，然后决定是输出0还是1的函数（即上图中Threshold T上方方框中的图形所代表的函数-跃迁函数）。但是由于跃迁函数不连续，不光滑，所以实际多采用下方的Sigmoid函数作为激活函数使用。

在计算机科学中，一个神经网络是包含了许多参数的数学模型，而这个数学模型又是由上述激活函数这样的若干个函数组成的。

感知机与多层网络

感知机由两层神经元组成，输入层接受到信号后传递给输出层（M-P神经元），他也被称为“阈值逻辑单元”，可以实现“与”、“或”、“非”的运算。

如上述M-P神经元抽象简化模型。

当x>或=0时，y=1，当x<0时，y=0

与：如果\[w_1=w_2=1,\theta=2\]，仅在\[x_1=x_2=1\]时，\[y=f(w_1*x_1+w_2*x_2-\theta)=f(0)=1\]

或：如果\[w_1=w_2=1,\theta=0.5\]，当\[x_1=1或者x_2=1\]时，\[y=f(1*x_1+1*x_2-0.5)=1\]

非：如果\[w_1=-0.6;w_2=0,\theta=-0.5\]，在\[x_1=1\]时，\[y=f(-0.6*x_1+0+0.5)=f(-0.1)=0\];在\[x_1=0\]时，\[y=f(0.5)=1\]

转载于:https://www.cnblogs.com/hankoui/p/6102743.html