二叉搜索树的遍历

最新推荐文章于 2025-06-24 18:19:30 发布

转载最新推荐文章于 2025-06-24 18:19:30 发布 · 105 阅读

0 ·

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/lzhxxyz/p/4857343.html

文章标签：

#数据结构与算法

二叉搜索树的遍历

1 二叉树的递归遍历

　　二叉树在数据结构中乃是重中之重，其应用非常广泛，很多数据结构都是建立在二叉树的基础上，如红黑色，平衡树等。

　　二叉树的定义如下：

　　　　一个有穷的结点集合。
　　　　这个集合可以为空。
　　　　若不为空，则它是由根结点和称为其左子树TL和右子树TR的两个不相交的二叉树组成。

　　可以看出，二叉树的定义是递归的。所以其递归遍历代码很容易理解。

// 二叉树节点
struct BinTreeNode
{
    int data;
    BinTreeNode *leftChild;
    BinTreeNode *rightChild;
};

1.1 前序遍历

　　前序遍历的访问顺序：根节点→左子树→右子树。

// 前序遍历
void preoder(BinTreeNode* bt)
{
    if (NULL != bt)
    {
        cout << bt->data << " ";

        preoder(bt->leftChild);
        preoder(bt->rightChild);
    }
}

1.2 中序遍历

　　中序遍历的访问顺序：左子树→根节点→右子树。

// 中序遍历
void inorder(BinTreeNode* bt)
{
    if (NULL != bt)
    {
        inorder(bt->leftChild);
        cout << bt->data << " ";
        inorder(bt->rightChild);
    }
}

1.3 后序遍历

　　后序遍历的访问顺序：左子树→右子树→根节点。

// 后序遍历
void postorder(BinTreeNode* bt)
{
    if (NULL != bt)
    {
        postorder(bt->leftChild);
        postorder(bt->rightChild);

        cout << bt->data << " ";
    }
}

2 二叉树的非递归遍历

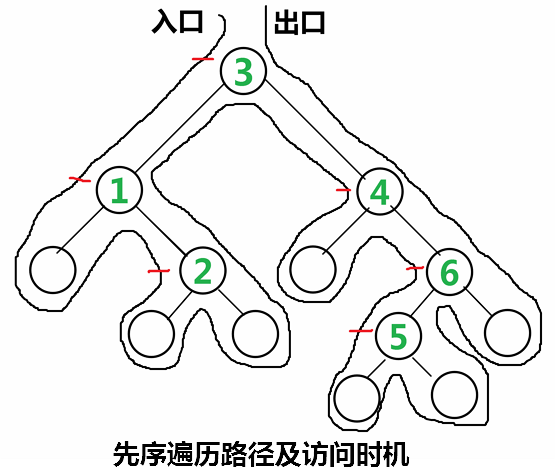
　　其实前序遍历、中序遍历和后序遍历的访问路径都是一样的，只是访问的时机不一样。如下图所示：

2.1 前序遍历

　　前序遍历的访问顺序：根节点→左子树→右子树。所以，对于每个节点，程序将在第1次遇到时就访问。

// 前序遍历
void preoder(BinTreeNode* bt)
{
    BinTreeNode *T = bt;
    stack<BinTreeNode*> st;

    while (T || !st.empty())
    {
        while (T)    
        {
            cout << T->data << " ";

            st.push(T);
            T = T->leftChild;
        }
        if (!st.empty())
        {
            T = st.top();
            st.pop();

            T = T->rightChild;
        }
    }
}

前序遍历

2.2 中序遍历

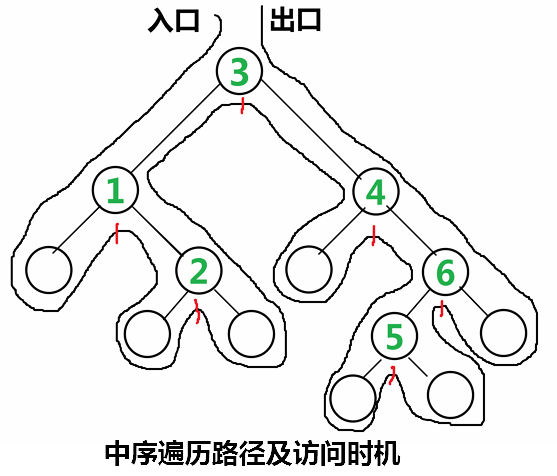
　　中序遍历的访问顺序：左子树→根节点→右子树。所以，对于每个节点，程序将在第2次遇到时才访问。

// 中序遍历
void inorder(BinTreeNode* bt)
{
    BinTreeNode *T = bt;
    stack<BinTreeNode*> st;

    while (T || !st.empty())
    {
        while (T)
        {
            st.push(T);
            T = T->leftChild;
        }
        if (!st.empty())
        {
            T = st.top();
            st.pop();
            cout << T->data << " ";

            T = T->rightChild;
        }
    }
}

中序遍历

2.3 后序遍历

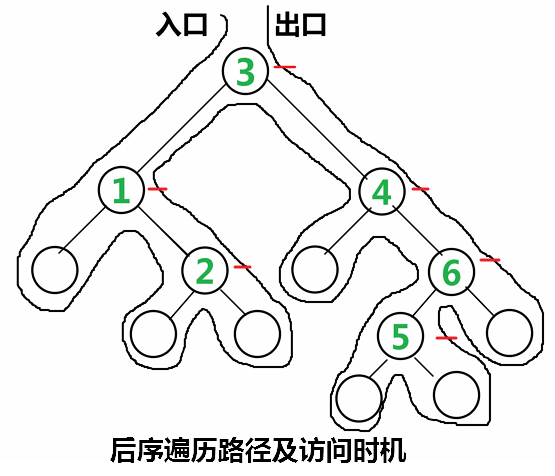
　　后序遍历的访问顺序：左子树→右子树→根节点。所以，对于每个节点，程序将在第3次遇到时才访问。这里，针对每个节点，将使用一个标示来记录节点的被遇到的次数。

// 后序遍历
void postorder(BinTreeNode* bt)
{
    BinTreeNode *T = bt;
    stack<BinTreeNode*> st;
    map<BinTreeNode*, int> visit;    // 用来记录每个节点被遇见的次数

    while (T || !st.empty())
    {
        while (T)
        {
            if (visit.find(T) == visit.end())    // 第1次遇到
            {
                visit[T] = 1;
                st.push(T);
            }
            T = T->leftChild;
        }

        if (!st.empty())
        {
            T = st.top();                        // 又遇见
            visit[T]++;

            if (3 == visit[T])                    // 如果第3次遇到，此时访问该节点
            {
                st.pop();
                cout << T->data << " ";
            }
            T = T->rightChild;
        }
    }
}

后序遍历

3 非递归遍历的完整代码

  1 #include "stdafx.h"
  2 #include <iostream>
  3 #include <stack>
  4 #include <map>
  5 
  6 using namespace std;
  7 
  8 // 二叉树节点
  9 struct BinTreeNode
 10 {
 11     int data;
 12     BinTreeNode *leftChild;
 13     BinTreeNode *rightChild;
 14 };
 15 
 16 
 17 void insertData(BinTreeNode * &bt, int data)
 18 {
 19     if (NULL == bt)
 20     {
 21         bt = new BinTreeNode();
 22 
 23         bt->data = data;
 24         bt->leftChild = NULL;
 25         bt->rightChild = NULL;
 26 
 27         return;
 28     }
 29     else
 30     {
 31         if (data < bt->data)
 32         {
 33             insertData(bt->leftChild, data);
 34         }
 35         else if (data > bt->data)
 36         {
 37             insertData(bt->rightChild, data);
 38         }
 39 
 40     }
 41 }
 42 
 43 
 44 // 遍历
 45 // 前序遍历
 46 void preoder(BinTreeNode* bt)
 47 {
 48     BinTreeNode *T = bt;
 49     stack<BinTreeNode*> st;
 50 
 51     while (T || !st.empty())
 52     {
 53         while (T)    
 54         {
 55             cout << T->data << " ";
 56 
 57             st.push(T);
 58             T = T->leftChild;
 59         }
 60         if (!st.empty())
 61         {
 62             T = st.top();
 63             st.pop();
 64 
 65             T = T->rightChild;
 66         }
 67     }
 68 
 69 }
 70 
 71 // 中序遍历
 72 void inorder(BinTreeNode* bt)
 73 {
 74     BinTreeNode *T = bt;
 75     stack<BinTreeNode*> st;
 76 
 77     while (T || !st.empty())
 78     {
 79         while (T)
 80         {
 81             st.push(T);
 82             T = T->leftChild;
 83         }
 84         if (!st.empty())
 85         {
 86             T = st.top();
 87             st.pop();
 88             cout << T->data << " ";
 89 
 90             T = T->rightChild;
 91         }
 92     }
 93 }
 94 
 95 // 后序遍历
 96 void postorder(BinTreeNode* bt)
 97 {
 98     BinTreeNode *T = bt;
 99     stack<BinTreeNode*> st;
100     map<BinTreeNode*, int> visit;    // 用来记录每个节点被遇见的次数
101 
102     while (T || !st.empty())
103     {
104         while (T)
105         {
106             if (visit.find(T) == visit.end())    // 第1次遇到
107             {
108                 visit[T] = 1;
109                 st.push(T);
110             }
111             T = T->leftChild;
112         }
113 
114         if (!st.empty())
115         {
116             T = st.top();                        // 又遇见
117             visit[T]++;
118 
119             if (3 == visit[T])                    // 如果第3次遇到，此时访问该节点
120             {
121                 st.pop();
122                 cout << T->data << " ";
123             }
124             T = T->rightChild;
125         }
126     }
127 }
128 
129 
130 int main()
131 {
132     int arr[6] = { 1, 2, 3, 5, 6, 4 };
133 
134     // 建立根节点
135     BinTreeNode *bt = new BinTreeNode();
136     bt->data = 3;
137     bt->leftChild = bt->rightChild = NULL;
138 
139 
140     // 插入元素
141     for (int i = 0; i < 6; i++)
142     {
143         insertData(bt, arr[i]);
144     }
145 
146     // 前序遍历
147     preoder(bt);
148     cout << endl;
149 
150     // 中序遍历
151     inorder(bt);
152     cout << endl;
153 
154     // 后序遍历
155     postorder(bt);
156     cout << endl;
157 
158     return 0;
159 }