嵌套矩形（动态规划）

最新推荐文章于 2020-10-21 10:55:01 发布

weixin_30906671

最新推荐文章于 2020-10-21 10:55:01 发布

阅读量232

点赞数

CC 4.0 BY-SA版权

文章标签：数据结构与算法

原文链接：http://www.cnblogs.com/ALINGMAOMAO/p/10798022.html

本文探讨了如何通过构建有向无环图(DAG)解决矩形排列问题，利用动态规划寻找最长递增子序列。文章详细介绍了算法思路，包括数据预处理、比较函数设计以及动态规划状态转移方程。

思路：

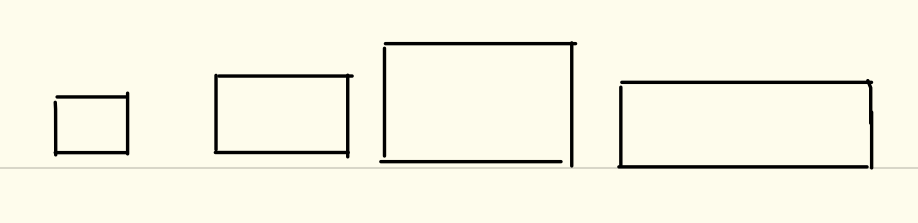先把这些矩形统一一下，让最长边向下，然后按大小放好。

这样，我们就可以来构建DAG图形，令，被包含的矩形a与包含的矩形b看成a一一>b的路线，这样就形成了这样的图形：

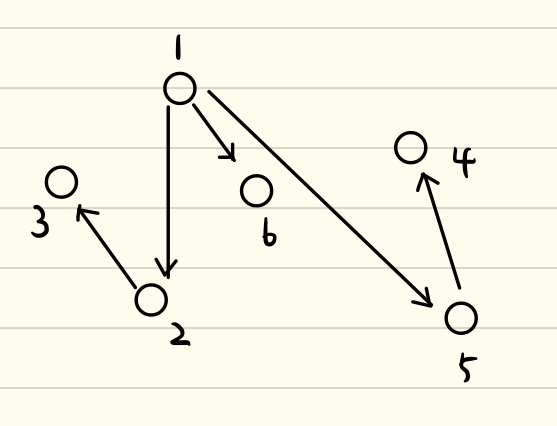，我们一定知道最小矩形一定是不能包含其他矩形的（因为没有矩形比最小矩形还小），同时，知道最大矩形一定不能被包含。（因为没有矩形比最大矩形大）

为什么，我们要考虑最大和最小矩形呢？

最小矩形和最大矩形是这整个dp的边界！同时，给出了dp的走势。

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int maxn = 1e3 + 10;
int dp[maxn], pre[maxn];
struct node{ int x, y; }a[maxn];
bool cmp(node a, node b){
    if (a.x == b.x)return a.y < b.y;
    return a.x < b.x;
}
int n, x, y;
int t;



int main(){
    cin >> t;
    while (t--){
        memset(dp, 0, sizeof(dp));
        cin >> n;
        for (int i = 1; i <= n; ++i)
        {
            cin >> x >> y;
            if (x < y)swap(x, y);
            a[i].x = x;        a[i].y = y;
            dp[i] = 1;
        }
        sort(a + 1, a + 1 + n, cmp);
//        for (int i = 1; i <= n; ++i)
//            cout << "(" << a[i].x << " ," << a[i].y << ")" << endl;

        for (int i = 1; i <= n - 1;++i)
        for (int j = i + 1; j <= n; ++j){
            if (a[i].x < a[j].x&&a[i].y < a[j].y){
                int sum = 1 + dp[i];
                if (dp[j] < sum){ dp[j] = sum; pre[j] = i; }
            }
        }
        int maxx = 1;
        for (int i = 1; i <= n;++i)
        if (dp[maxx] < dp[i])maxx = i;
    //    Path(maxx);  cout << endl;
        cout << dp[maxx] << endl;
    }
}