LeetCode 62. Unique Paths 唯一路径

最新推荐文章于 2025-04-02 22:31:45 发布

weixin_30906185

最新推荐文章于 2025-04-02 22:31:45 发布

阅读量69

点赞数

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/CloudFlew/p/5162025.html

本文探讨了使用递归和动态规划方法解决迷宫问题，详细介绍了三种求解路径数量的方法，并通过LeetCode实例进行说明。从自上而下的递归到自下而上的循环，再到利用杨辉三角简化计算，最终采用阶乘计算优化实现高效求解。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

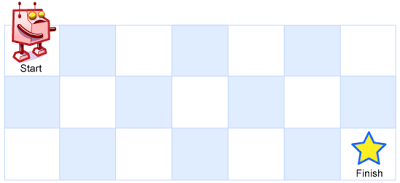
题目: 一个机器人位于 m x n 网格的右上角. 机器人只能向右或者向下. 机器人试图到达右下角. 问有多少种不重复的路径?
上图是一个 3 x 7 的网格. m 和 n 最大为 100.
链接: https://leetcode.com/problems/unique-paths/

方法一: 自上而下的递归

如图, 到达 Finish 点 (3, 7) 的所有不重复路径个数等于到达点 (3, 6) 的路径个数加上到达点 (2, 7) 的路径个数. 同理: (3, 6) = (3, 5) + (2, 6) .....
当 m = 1 或 n = 1 时, 只有一条路径. 这是递归的终止条件.
具体的代码如下:

    public int uniquePaths(int m, int n) {
        if (m == 1 || n == 1)
            return 1;
        else
            return uniquePaths(m - 1, n) + uniquePaths(m, n - 1);
    }

LeetCode 上提交后显示超时了, 预料之中.... 一般有返回值的递归都比较耗时, 因为要保存所有的未计算的节点.

方法二: 自下而上的循环

自上而下的递归不行, 我们可以尝试自下而上的循环, 把每一次的计算结果保存在二维数组中.例如 matrix[1][2] = 3 代表从 (1, 1) 到达 (2, 3) 共有 3 种不同的路径(数组下标从 0 开始, 所以 (m, n) 对应 matrix[m-1][n-1]). 从 matrix[0][0] 一直计算到 matrix[99][99], 因为 LeetCode 测试用例有几十个, 所以将计算结果保存到静态成员变量中, 只计算一次就可以了.

    static int[][] matrix = new int[100][100];
    static {
        matrix[0][0] = 1;
        for (int i = 1; i < 100; i++) {
            matrix[i][0] = 1;
            matrix[0][i] = 1;
        }
        for (int m = 1; m < 100; m++) {
            for (int n = 1; n < 100; n++) {
                matrix[m][n] = matrix[m][n - 1] + matrix[m - 1][n];
            }
        }
    }
    // 自下而上把算出来的值存入二维数组中(100X100),然后直接取用
    public int uniquePaths2(int m, int n) {
        return matrix[m - 1][n - 1];
    }

提交后显示用时 9ms,仍然不够快.

方法三

把我们得到的二维数组打印出来, 看看有什么规律没有: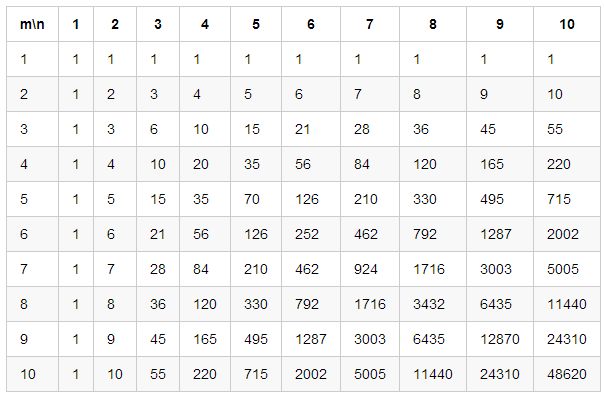

斜着看这不就是杨辉三角吗! 坑啊...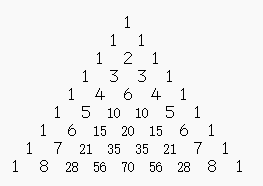

其中, 计算方法为:
$mathtex.cgi?%20%5CLarge%20C%7B%5Ek_n%7D=%5Cfrac%7Bn!%7D%7B(n-k)!*k!%7D%20$

(m, n) 对应于上图的第 (m+n-2) 行, 第 (n-1) 列

    public int uniquePaths3(int m, int n) {
        if (m == 1 || n == 1)
            return 1;
        if (m == 2 || n == 2)
            return m >= n ? m : n;
        if (m >= n)
            return (int) (f( m + n - 2, m) / f( n - 1, 1));
        else
            return (int) (f( m + n - 2, n) / f( m - 1, 1));
    }
 
    //阶乘.不能用 int, 因为 13 的阶乘就超过 int 的范围了
    public static long f(int a, int b) {
    long result = (long) a;
    for (int i = a - 1; i > b - 1; i--)
        result *=  i;
    return result;
    }

提交后显示用时 0 ms, 够快了.

转载于:https://www.cnblogs.com/CloudFlew/p/5162025.html