POJ 3347 Kadj Squares （计算几何）

最新推荐文章于 2020-06-27 15:33:17 发布

转载最新推荐文章于 2020-06-27 15:33:17 发布 · 106 阅读

0 ·

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/whdsunny/p/9879367.html

本文介绍了一种算法，用于确定当多个不同大小的正方形按特定规则放置在平面上时，从上方视角哪些正方形是可见的。通过计算每个正方形的左、右边界，并考虑它们之间的相对位置和大小，该算法能够找出所有可见正方形的索引。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题目：

Description

In this problem, you are given a sequence S₁, S₂, ..., S_n of squares of different sizes. The sides of the squares are integer numbers. We locate the squares on the positive x-y quarter of the plane, such that their sides make 45 degrees with x and y axes, and one of their vertices are on y=0 line. Let b_i be the x coordinates of the bottom vertex of S_i. First, put S₁ such that its left vertex lies on x=0. Then, put S₁, (i > 1) at minimum b_i such that

b_i > b_i_-1 and
the interior of S_i does not have intersection with the interior of S₁...S_i-1.

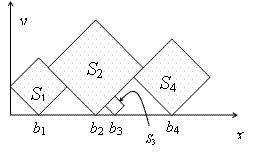
The goal is to find which squares are visible, either entirely or partially, when viewed from above. In the example above, the squares S₁, S₂, and S₄ have this property. More formally, S_i is visible from above if it contains a point p, such that no square other than S_i intersect the vertical half-line drawn from p upwards.

Input

The input consists of multiple test cases. The first line of each test case is n (1 ≤ n ≤ 50), the number of squares. The second line contains n integers between 1 to 30, where the ith number is the length of the sides of S_i. The input is terminated by a line containing a zero number.

Output

For each test case, output a single line containing the index of the visible squares in the input sequence, in ascending order, separated by blank characters.

Sample Input

Sample Output

1 2 4
1 3

题意:依次给出n个正方形的边长 每个正方形在x轴上呈45°摆放并且尽可能放的紧凑 问从上方看时能看见哪些正方形
思路：对于第i个正方形 判断前i-1个正方形如果和它相交的话左端点的位置 最后取一个最大值作为整个正方形的左端点位置
　　　对于j<i的正方形 如果i的边长大于j 那么j的最右能看到的部分就不会比i的最左端点大 反之 i的最左能看到的部分就不会比j最右端点小
　　  再将最左能看到的端点比最右能看到的端点去掉
　　  为了避免浮点数 将每条边乘上sqrt(2)然后约掉 效果等于将正方形投影到x轴上

代码：

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <string>
#include <cstring>
#include <algorithm>

using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const int inf=0x3f3f3f3f;
const int maxn=110;
int n;

struct node{
    int l,r,len;
}kk[maxn];

int main(){
    while(~scanf("%d",&n)){
        if(n==0) break;
        for(int i=1;i<=n;i++){
            scanf("%d",&kk[i].len);
            kk[i].l=0;
            for(int j=1;j<i;j++){
                kk[i].l=max(kk[i].l,kk[j].r-abs(kk[i].len-kk[j].len));
            }          
            kk[i].r=kk[i].l+2*kk[i].len;
        }
        for(int i=1;i<=n;i++){
            for(int j=1;j<i;j++){
                if(kk[i].l<kk[j].r && kk[i].len<kk[j].len)
                    kk[i].l=kk[j].r;
            }
            for(int j=i+1;j<=n;j++){
                if(kk[i].r>kk[j].l && kk[i].len<kk[j].len)
                    kk[i].r=kk[j].l;
            }
        }
        int flag=1;
        for(int i=1;i<=n;i++){
            if(kk[i].l<kk[i].r){
                if(flag) flag=0;
                else printf(" ");
                printf("%d",i);
            }
        }
        printf("\n");
    }
    return 0;
}

转载于:https://www.cnblogs.com/whdsunny/p/9879367.html