网络流练习

最新推荐文章于 2025-01-02 16:07:04 发布

转载最新推荐文章于 2025-01-02 16:07:04 发布 · 62 阅读

0 ·

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/ZUTTER/p/10040439.html

本文深入探讨了最大流算法在各种场景中的应用，包括但不限于餐饮搭配、矩阵游戏、士兵占领问题等，通过具体实例讲解如何构建网络流模型，解决实际问题。

Dining

原点连饮料，饮料连牛，牛连食物

但是这样是错的，因为不能保证每头牛只被匹配一次

所以把牛拆开限流量1即可

#include<iostream>
#include<cstdio>
#include<queue>
#include<vector>
#include<cstring>
#define M 1000000
using namespace std;

int d[M],i,m,n,j,k,ver[M],edge[M],head[M],nex[M],cnt=1,s,t,p,v[101],ans,x,y;
queue <int> q;

void add(int x,int y,int z)
{
    ver[++cnt]=y; edge[cnt]=z; nex[cnt]=head[x]; head[x]=cnt;
    ver[++cnt]=x; edge[cnt]=0; nex[cnt]=head[y]; head[y]=cnt;
}

bool bfs()
{
    memset(d,0,sizeof(d));
    while(q.size()) q.pop();
    q.push(0); d[0]=1;
    while(q.size())
    {
        int x=q.front(); q.pop();
        for(int i=head[x];i;i=nex[i])
        if(edge[i] && !d[ver[i]])
        {
            q.push(ver[i]);
            d[ver[i]]=d[x]+1;
            if(ver[i]==t) return 1;
        }
        
    }
    return 0;
}

int dinic(int x,int flow)
{
    if(x==t) return flow;
    int re=flow, k;
    for(int i=head[x];i && re;i=nex[i])
    if(edge[i] && d[ver[i]]== d[x]+1)
    {
        k=dinic(ver[i], min(re,edge[i]));
        if(!k) d[ver[i]]=0;
        edge[i]-=k;
        re-=k;
        edge[i^1]+=k;
    }
    return flow-re;
}

int main()
{
    
    scanf("%d%d%d",&n,&p,&m);
    t=n+n+p+m+1;
    for(i=n+n+1;i<=n+n+p;i++) add(0,i,1);
    for(i=n+n+p+1;i<=n+n+p+m;i++) add(i,t,1);
    for(i=1;i<=n;i++) add(i,i+n,1);
    
    for(i=1;i<=n;i++) 
    {
        scanf("%d%d",&x,&y);
        for(j=1;j<=x;j++)
        {
            scanf("%d",&k);
            add(n+n+k,i,1);
        }
        for(j=1;j<=y;j++) 
        {
            scanf("%d",&k);
            add(i+n,n+n+p+k,1);
        }
    }

    while(bfs()) 
    {
        k=dinic(0,0x3f3f3f3f);
        ans+=k;
        if(!k) break;
    }

    printf("%d",ans);
}

小凸玩矩阵

把行和列拆开看成二分图，再二分\(check\)一下看看能不能选到\(n-k\)个比\(mid\)小的数

#include<iostream>
#include<cstdio>
#include<queue>
#include<vector>
#include<cstring>
#define M 1000000
using namespace std;

int a[M],d[M],i,m,n,j,k,ver[M],edge[M],head[M],nex[M],cnt=1,s,t,p,ans,x,y,cost[M],r,l=0x3f3f3f3f,cur[M];
queue <int>q;

inline void add(int x,int y,int z)
{
    ver[++cnt]=y; nex[cnt]=head[x]; head[x]=cnt; edge[cnt]=1; cost[cnt]=z;
    ver[++cnt]=x; nex[cnt]=head[y]; head[y]=cnt; edge[cnt]=0; cost[cnt]=z;
}

bool bfs(int z)
{
    memset(d,0,sizeof(d));
    for(i=0;i<=t;i++) cur[i]=head[i];
    while(q.size()) q.pop();
    q.push(0); d[0]=1;
    while(q.size())
    {
        int x=q.front(); q.pop();
        for(int i=head[x];i;i=nex[i])
        if(edge[i] && !d[ver[i]] && cost[i]<=z) 
        {
            q.push(ver[i]);
            d[ver[i]]=d[x]+1;
            if(ver[i]==t) return 1;
        }
    }
    return 0;
}

int dinic(int x,int flow,int z)
{
    int re=flow;
    if(x==t) return flow;
    if(!flow) return 0;
    for(int& i=cur[x];i;i=nex[i])
    if(edge[i]==1 && d[ver[i]]==d[x]+1 && cost[i]<=z)
    {
        //cur[x]=i;
        int s=dinic(ver[i],min(re, edge[i]),z);
        if(!s) d[ver[i]]=0;
        edge[i]-=s; edge[i^1]+=s;
        re-=s;
        if(!re) break;
    }
    return flow-re;
}

bool check(int x)
{
    int ans=0;
    while(bfs(x)) 
        while(s=dinic(0,0x3f3f3f3f,x)) ans+=s;
    for(int i=1;i<=cnt;i++) if(!(i&1)) edge[i]=1; else edge[i]=0;
    if(ans>=n-k+1) return 1;
    return 0;
}

int erfen()
{
    int tmp=r;
    while(l<=r)
    {
        int mid=(l+r)>>1;
        if(check(mid)) tmp=mid, r=mid-1;
        else l=mid+1;
    }
    return tmp;
}


int main()
{
    scanf("%d%d%d",&n,&m,&k);
    t=n+m+1;
    for(i=1;i<=n;i++) add(0,i,0);
    for(i=1;i<=m;i++) add(n+i,t,0);
    for(i=1;i<=n;i++)
        for(j=1;j<=m;j++)
        {
            scanf("%d",&s);
            add(i,n+j,s);   
            r=max(r,s);
            l=min(l,s);
        }
        
    printf("%d",erfen());
}

士兵占领

同样是把行和列拆开，由于要求的是最小值，可以转化为\(sum-\)一个最大值，就可以跑最大流啦

#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
#define M 110
using namespace std;

int d[M<<10],ans,a[M][M],s,t,n,m,k,c[M],l[M],head[M<<10],edge[M<<10],nex[M<<10],ver[M<<10],cnt=1,cur[M<<10],cnx[M],cny[M];
queue<int> q;
void add(int x,int y,int z)
{
    ver[++cnt]=y; nex[cnt]=head[x]; head[x]=cnt; edge[cnt]=z;
    ver[++cnt]=x; nex[cnt]=head[y]; head[y]=cnt; edge[cnt]=0;
}

int dinic(int x,int flow)
{
    if(x==t || !flow) return flow;
    int re=flow, k;
    for(int& i=cur[x];i && re;i=nex[i])
    if(edge[i]>0 && d[ver[i]]==d[x]+1)
    {
        k=dinic(ver[i],min(re,edge[i]));
        if(!k) d[ver[i]]=0;
        re-=k; edge[i]-=k; edge[i^1]+=k;
        if(!re) break;
    }
    return flow-re;
}

bool bfs()
{
    memset(d,0,sizeof(d));
    while(q.size()) q.pop();
    for(int i=0;i<=t;i++) cur[i]=head[i];
    q.push(0); d[0]=1;
    while(q.size())
    {
        int x=q.front(); q.pop();
        for(int i=head[x];i;i=nex[i])
        if(edge[i]>0 && !d[ver[i]])
        {
            d[ver[i]]=d[x]+1;
            q.push(ver[i]);
            if(ver[i]==t) return 1;
        }
    }
    return 0;
}

int main()
{
    scanf("%d%d%d",&n,&m,&k);
    t=n+m+1;
    for(int i=1;i<=n;i++) scanf("%d",&l[i]);
    for(int i=1;i<=m;i++) scanf("%d",&c[i]);
    s=n*m-k;
    for(int i=1;i<=k;i++)
    {
        int x,y;
        scanf("%d%d",&x,&y);
        a[x][y]=1;
        cnx[x]++; cny[y]++;
    }
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
            if(!a[i][j]) add(i,n+j,1);
    for(int i=1;i<=n;i++) 
        if(m-l[i]-cnx[i]<0) 
        {
            printf("JIONG!");
            return 0;
        }
        else add(0,i,m-l[i]-cnx[i]);
    for(int i=1;i<=m;i++) 
        if(n-c[i]-cny[i]<0)
        {
            printf("JIONG!");
            return 0;
        }
        else add(i+n,t,n-c[i]-cny[i]);
    while(bfs())
        while(1)
        {
        
            k=dinic(0,0x3f3f3f3f);
            ans+=k;
            if(!k) break;
        }
    printf("%d",s-ans);
}

Collectors Problem

对于每个贴纸和\(Bob\)的每个朋友建点

由每种贴纸向汇点连流量为\(1\)的边
原点向每种贴纸连流量为\(Bob\)此种贴纸个数的边
如果一位朋友拥有一种贴纸超过一张，由他向那种贴纸连贴纸个数-1的边
如果一位朋友没有一种贴纸，由那种贴纸向他连1的边

跑最大流即可~

#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
#define M 100000
using namespace std;

queue<int> q; 
int d[M],i,m,n,j,k,a[100][100],head[M],edge[M],ver[M],nex[M],s,t,z,cur[M],b[M],cnt,ans;

void add(int x,int y,int z)
{
    ver[++cnt]=y; nex[cnt]=head[x]; head[x]=cnt; edge[cnt]=z;
    ver[++cnt]=x; nex[cnt]=head[y]; head[y]=cnt; edge[cnt]=0;
}

int dinic(int x,int flow)
{
    if(x==t || !flow) return flow;
    int re=flow, k;
    for(int& i=cur[x];i && re;i=nex[i])
    if(edge[i] && d[ver[i]]==d[x]+1)
    {
        k=dinic(ver[i],min(re, edge[i]));
        if(!k) d[ver[i]]=0;
        re-=k; edge[i]-=k; edge[i^1]+=k;
        if(!re) break;
    }
    return flow-re;
}

bool bfs()
{
    memset(d,0,sizeof(d));
    for(int i=0;i<=t;i++) cur[i]=head[i];
    while(q.size()) q.pop();
    q.push(0); d[0]=1;
    while(q.size())
    {
        int x=q.front(); q.pop();
        for(int i=head[x];i;i=nex[i])
        if(edge[i] && !d[ver[i]])
        {
            d[ver[i]]=d[x]+1;
            q.push(ver[i]);
            if(ver[i]==t) return 1;
        }
    }
    return 0;
}
int main()
{
    scanf("%d",&z);
    for(int u=1;u<=z;u++)
    {
        memset(head,0,sizeof(head));
        memset(nex,0,sizeof(nex));
        memset(a,0,sizeof(a));
        cnt=1; ans=0;
        
        scanf("%d%d",&n,&m);
        t=n+1+m;
        for(int i=1;i<=m;i++) add(i,t,1);
        for(int i=1;i<=n;i++)
        {
            scanf("%d",&a[i][0]);
            for(int j=1;j<=a[i][0];j++) 
            {
                int k;
                scanf("%d",&k);
                a[i][k]++;
            }
            if(i==1) {for(int j=1;j<=m;j++) if(a[i][j]) add(0,j,a[i][j]);}
            else for(int j=1;j<=m;j++)
            {   
                if(a[i][j]>1) add(m+i,j,a[i][j]-1);
                else if(!a[i][j]) add(j,m+i,1);
            }
        }
        while(bfs())
        {
            while(k=dinic(0,0x3f3f3f3f)) 
                ans+=k;
        }
        printf("Case #%d: %d\n",u,ans);
    }
    return 0;
}

试题库

对所属类别建点，每到题建点，原点流向类别的容量是所需题数，再从每种类别向它包含的题连边，每道题向汇点连容量为1的边，如果最大流是m就有解，从每个汇点看它到非原点那个点没有流量就是以组解啦

#include<iostream>
#include<cstdio>
#include<queue>
#include<cstring>
#define M 2000001
using namespace std;

int d[M],t,i,m,n,j,k,head[M],edge[M],nex[M],ver[M],cnt=1,s,a[M],p,ans,u,cur[M];
queue<int> q;
void add(int x,int y,int z)
{
    ver[++cnt]=y; nex[cnt]=head[x]; head[x]=cnt; edge[cnt]=z;
    ver[++cnt]=x; nex[cnt]=head[y]; head[y]=cnt; edge[cnt]=0;
}

int dinic(int x,int flow)
{
    if(x==t|| !flow) return flow;
    int re=flow, k;
    for(int& i=cur[x];i && re;i=nex[i])
    if(edge[i] && d[ver[i]]==d[x]+1)
    {
        k=dinic(ver[i],min(re, edge[i]));
        re-=k; edge[i]-=k; edge[i^1]+=k;
    }
    return flow-re;
}

bool bfs()
{
    while(q.size()) q.pop();
    memset(d,0,sizeof(d)); 
    memcpy(cur,head,sizeof(head));
    q.push(0); d[0]=1;
    while(q.size())
    {
        int x=q.front(); q.pop();
        for(int i=head[x];i;i=nex[i])
        if(edge[i] && !d[ver[i]])
        {
            d[ver[i]]=d[x]+1;
            if(ver[i]==t) return 1;
            q.push(ver[i]);
        }   
    }
    return 0;
}

int main()
{
    scanf("%d%d",&k,&n);
    t=k+n+1;
    for(int i=1;i<=k;i++)
    {
        scanf("%d",&s);
        m+=s;
        add(0,n+i,s);
    } 
    for(int i=1;i<=n;i++)
    {
        add(i,t,1);
        scanf("%d",&p);
        for(;p;p--) scanf("%d",&s), add(n+s,i,1);
    }
    while(bfs()) while(u=dinic(0,0x3f3f3f3f)) ans+=u;
    if(ans!=m)
    {
        printf("No Solution!");
        return 0;
    }
    for(int x=n+1;x<=n+k;x++)
    {
        printf("%d:",x-n);
        for(int i=head[x];i;i=nex[i]) if(ver[i]!=0 && !edge[i]) printf(" %d",ver[i]);
        printf("\n");
    }
    
}

方格取数问题

先对棋盘黑白染色，就会变成二分图上的最小割啦

从原点到每个白点连边，容量是白点权值，白点向与它有边相连的黑点连边，边权\(inf\)黑点再向汇点连权值的边

#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
#define M 500000
using namespace std;

int n,m,k,head[M],edge[M],ver[M],nex[M],cnt=1,t,d[M],cn,sum,ans,cur[M],b[M];
queue<int> q;

void add(int x,int y,int z)
{
    ver[++cnt]=y; nex[cnt]=head[x]; head[x]=cnt; edge[cnt]=z; 
    ver[++cnt]=x; nex[cnt]=head[y]; head[y]=cnt; edge[cnt]=0;
}

int dinic(int x,int flow)
{
    if(x==t || !flow) return flow;
    int re=flow,k;
    for(int& i=cur[x];i && re;i=nex[i])
    if(edge[i] && d[ver[i]]==d[x]+1)
    {
        k=dinic(ver[i],min(re,edge[i]));
        re-=k; edge[i]-=k; edge[i^1]+=k;
    } 
    return flow-re;
}

bool bfs()
{
    while(q.size()) q.pop();
    memset(d,0,sizeof(d));
    q.push(0); d[0]=1;
    memcpy(cur,head,sizeof(head));
    while(q.size())
    {
        int x=q.front(); q.pop();
        for(int i=head[x];i;i=nex[i])
        if(edge[i] && !d[ver[i]])
        {
            d[ver[i]]=d[x]+1;
            if(ver[i]==t) return 1;
            q.push(ver[i]);
        }
    }
    return 0;
}

int main()
{
    scanf("%d%d",&n,&m);
    t=n*m+1;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++) 
        {
            cn+=1;
            scanf("%d",&k); sum+=k;
            if((i==1 && (cn%2)) || (i!=1 && (!b[cn-m]))) add(0,cn,k),b[cn]=1;
            else {add(cn,t,k); continue;}
            if(i!=n) add(cn,cn+m,0x3f3f3f3f);
            if(i!=1) add(cn,cn-m,0x3f3f3f3f);
            if(j!=1) add(cn,cn-1,0x3f3f3f3f);
            if(j!=m) add(cn,cn+1,0x3f3f3f3f);
        }
    while(bfs()) while(k=dinic(0,0x3f3f3f3f)) ans+=k; 
    printf("%d",sum-ans);
}

3532: [Sdoi2014]Lis

给定序列A，序列中的每一项Ai有删除代价Bi和附加属性Ci。请删除若干项，使得4的最长上升子序列长度减少至少1，且付出的代价之和最小，并输出方案。
如果有多种方案，请输出将删去项的附加属性排序之后，字典序最小的一种。

按在上升子序列中的位置连成网络，拆点之间限流为\(b\),显然跑一波最小割最长上升子序列长度就会减一

但是字典序最小的割边要怎么找呢QAQ

如果一条正向边满流了而且在残图中这条边的起点到终点不连通那么这条边就可以是割边

当然了啊如果这条边甚至没有满流它怎么可能成为割边，如果去掉这条边还是联通那去掉了也没有什么用同样不可能是割边

然后就把序列按照c排序，把拆出来的\(n\) 条边先连上，然后一个个判断这条边是不割边。

注意判断是割边后要把这条边退流，这样的话和这条边在同一条路径上的边就不会被选重了

这样是可以保证字典序最小的，每一个长度能到达答案的上升序列都包含一个被流掉的点，贪心并不会使后面的边的选择变劣

#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
#include<algorithm>
#define M 150000
using namespace std;

int n,m,k,t,ver[M],edge[M],head[M],nex[M],cnt=1,c[M],T,ans,cur[M],d[M],maxx,fr[M],p[M],l;
queue <int> q;

struct vv
{
    int a,b,c,w,f;
} v[M];

bool cmp(vv a,vv b) {return a.c<b.c;}
void modi(int x,int k){for(int i=x;i<=n;i+=i & -i) c[i]=max(c[i],k);}
int ask(int x){int ans=0; for(int i=x;i>0;i-=i & -i) ans=max(ans,c[i]); return ans;}
void add(int x,int y,int z)
{
    ver[++cnt]=y; nex[cnt]=head[x]; head[x]=cnt; edge[cnt]=z; fr[cnt]=x;
    ver[++cnt]=x; nex[cnt]=head[y]; head[y]=cnt; edge[cnt]=0;
}

bool bfs(int S,int T)
{
    memcpy(cur,head,sizeof(head));
    memset(d,0,sizeof(d));
    while(q.size()) q.pop();
    d[S]=1; q.push(S);
    while(q.size())
    {
        int x=q.front(); q.pop();
        for(int i=head[x];i;i=nex[i])
        if(edge[i] && !d[ver[i]])
        {
            d[ver[i]]=d[x]+1;
            if(ver[i]==T) return 1;
            q.push(ver[i]);
        }
    }
    return 0;
}

int dinic(int x,int flow,int T)
{
    if(x==T || !flow) return flow;
    int re=flow, k;
    for(int& i=cur[x];i && re;i=nex[i])
    if(edge[i] && d[ver[i]]==d[x]+1)
    {
        int k=dinic(ver[i],min(re,edge[i]),T);
        re-=k; edge[i]-=k; edge[i^1]+=k;
        if(!k) d[ver[i]]=0;
    } 
    return flow-re;
}

int main()
{
    scanf("%d",&T);
    for(;T;T--)
    {
        memset(head,0,sizeof(head)); memset(nex,0,sizeof(nex));
        cnt=1, ans=maxx=l=0; memset(c,0,sizeof(c));
        scanf("%d",&n); t=2*n+1;
        for(int i=1;i<=n;i++) scanf("%d",&v[i].a);
        for(int i=1;i<=n;i++) scanf("%d",&v[i].b);
        for(int i=1;i<=n;i++) scanf("%d",&v[i].c), v[i].w=i;
        for(int i=1;i<=n;i++)
        {
            v[i].f=ask(v[i].a-1)+1; maxx=max(maxx,v[i].f);
            modi(v[i].a,v[i].f);
        }
        sort(v+1,v+1+n,cmp);
        for(int i=1;i<=n;i++) add(v[i].w,v[i].w+n,v[i].b);
        for(int i=1;i<=n;i++)
        {
            for(int j=1;j<=n;j++) if(v[j].w>v[i].w && v[j].f==v[i].f+1 && v[j].a>v[i].a) 
                add(v[i].w+n,v[j].w,0x3f3f3f3f);
            if(v[i].f==1) add(0,v[i].w,0x3f3f3f3f);
            if(v[i].f==maxx) add(v[i].w+n,t,0x3f3f3f3f);
        }
        while(bfs(0,t)) while(k=dinic(0,0x3f3f3f3f,t)) ans+=k;
        for(int i=2;i<=n+n+2;i+=2) 
        if(!edge[i] && ver[i]==fr[i]+n && fr[i]  &&!bfs(fr[i],ver[i]))
        {
            p[++l]=fr[i];
            bfs(fr[i],0); while(dinic(fr[i],edge[i^1],0));
            bfs(t,ver[i]); while(dinic(t,edge[i^1],ver[i]));
        }
        sort(p+1,p+1+l);
        printf("%d %d\n",ans,l);
        for(int i=1;i<=l;i++)  printf("%d ",p[i]);
        printf("\n");
    }
}

3130: [Sdoi2013]费用流

略一分析我们只要给流量最大的边加一个p的费用就行了啊

但是怎么找流量最大的边呢

二分啊！！

先跑出最大流然后枚举mid，如果把所有边的流量都控制在mid一下最大流不变就说明mid可行

但这是不是有点太简单了？？

认真读一遍题，发现这题甚至没有要求流量是整数！！！！

然后改成实数

然后就没了

#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
#include<cmath>
#include<algorithm>
#define M 1000001
#define MP make_pair
#define TS q.top().second
#define D 1e-4
using namespace  std;

int n,m,ver[M], head[M],nex[M],cnt=1,d[M],g[M],p,t,x,y,z,k,maxx,ans,cur[M];
double edge[M],e[M],s;
queue <int>q;

bool pan(double a,double b)
{
    if(a>b) return (a-b)<=D;
    else return b-a<=D;
}

void add(int x,int y,int z)
{
    ver[++cnt]=y; nex[cnt]=head[x]; head[x]=cnt; edge[cnt]=z*1.0;
    ver[++cnt]=x; nex[cnt]=head[y]; head[y]=cnt; edge[cnt]=0.0;
}

bool bfs()
{
    memset(d,0,sizeof(d)); while(q.size())q.pop();
    d[1]=1; q.push(1); memcpy(cur,head,sizeof(head));
    while(q.size())
    {
        int x=q.front(); q.pop();
        for(int i=head[x];i;i=nex[i])
        if(edge[i] && !d[ver[i]])
        {
            d[ver[i]]=d[x]+1;
            q.push(ver[i]);
        }
    }
    if(d[t]) return 1;
    return 0;
}

double dinic(int x,double flow)
{
    if(x==t || !flow) return flow;
    double re=flow, k;
    for(int& i=cur[x];i && re;i=nex[i])
    if(edge[i] && d[ver[i]]==d[x]+1 )
    {
        k=dinic(ver[i],min(re,edge[i]));
        if(!k) d[ver[i]]=0;
        re-=k; edge[i]-=k; edge[i^1]+=k;
    }
    return flow-re;
}

bool check(double x)
{
    double r=0;
    memcpy(edge,e,sizeof(e));
    for(int i=2;i<=cnt;i++) edge[i]=min(edge[i],x);
    while(bfs()) while(s=dinic(1,0x3f3f3f3f*1.0)) r+=s;
    return pan(r,ans*1.0);
}

double ef(double l,double r)
{
    double mid,tmp=r;
    while(l<=r)
    {
        mid=(l+r)/2;
        if(check(mid)) tmp=mid, r=mid-1;
        else l=mid+1;
    }
    return tmp;
}

int main()
{
    scanf("%d%d%d",&n,&m,&p); t=n;
    for(int i=1;i<=m;i++)
    {
        scanf("%d%d%d",&x,&y,&z);
        add(x,y,z); maxx=max(maxx,z);
    }
    memcpy(e,edge,sizeof(edge));
    while(bfs()) while(k=dinic(1,0x3f3f3f3f)) ans+=k;
    printf("%d\n",ans);
    printf("%.4lf",1.0*ef(0,maxx)*p);
    
}

1059: [ZJOI2007]矩阵游戏

Too young too simple 的思想历程

一共有n个黑子就一定有解!(...)

(随便hack一下

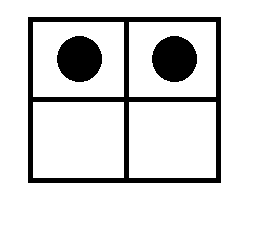
每行都有黑子就有解！（。。。）

（太蠢了不说了
每行每列都有黑子就有解！

还是不对啊！比如说

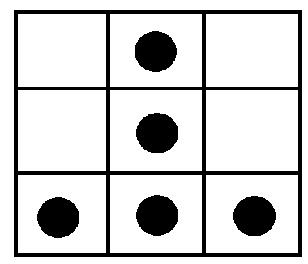
就显然还是没解
正解：存在n个点，x坐标和y坐标分别不相同

这里显然可以用二分图匹配！

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<queue>
#include<cstring>
#define M 1000001
using namespace std;

int t,m,n,k,d[M],ver[M],edge[M],nex[M],cnt,head[M],cur[M];
queue <int> q;
void add(int x,int y)
{
    ver[++cnt]=y; nex[cnt]=head[x]; head[x]=cnt; edge[cnt]=1;
    ver[++cnt]=x; nex[cnt]=head[y]; head[y]=cnt; edge[cnt]=0;
}

bool bfs()
{
    while(q.size()) q.pop();
    memset(d,0,sizeof(d)); memcpy(cur,head,sizeof(head));
    d[0]=1; q.push(0);
    while(q.size())
    {
        int x=q.front(); q.pop();
        for(int i=head[x];i;i=nex[i])
        if(!d[ver[i]] && edge[i])
        {
            d[ver[i]]=d[x]+1;
            if(ver[i]==t) return 1;
            q.push(ver[i]);
        }
    }
    return 0;
}

int dinic(int x,int flow)
{
    if(!flow || x==t) return flow;
    int re=flow, k;
    for(int& i=cur[x];i && re;i=nex[i])
    if(edge[i] && d[ver[i]]==d[x]+1)
    {
        k=dinic(ver[i],min(re,edge[i]));
        re-=k; edge[i]-=k; edge[i^1]+=k; 
    }
    return flow-re;
}

平面图转对偶图

1001: [BeiJing2006]狼抓兔子

很容易想到最小割，但是\(10^6\)显然没什么前途

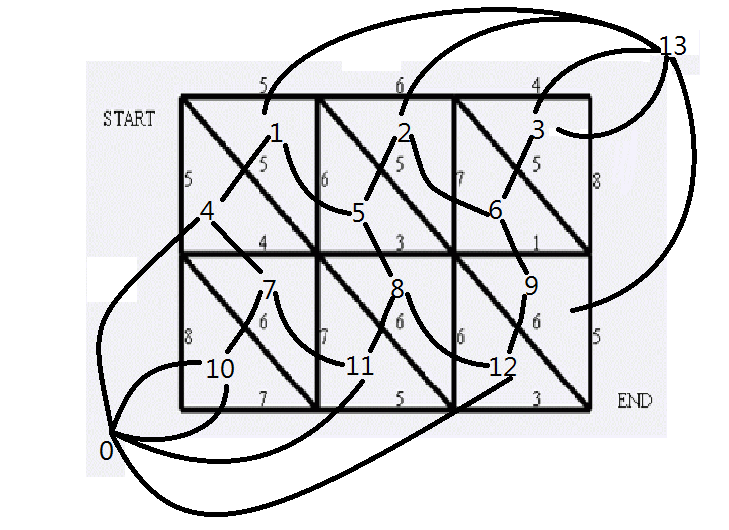
然后从0到13跑最短路就行啦

#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
#define M 6000001
using namespace std;

int inq[M],n,m,head[M],edge[M],ver[M],nex[M],cnt,k,a[M];
queue <int>q;
void add(int x,int y,int z)
{
    ver[++cnt]=y; nex[cnt]=head[x]; head[x]=cnt; edge[cnt]=z;
    ver[++cnt]=x; nex[cnt]=head[y]; head[y]=cnt; edge[cnt]=z;
}

int main()
{
    scanf("%d%d",&n,&m);
    int z=m-1; int t=(n-1)*z*2+1;
    for(int i=0;i<n;i++) 
        for(int j=1;j<m;j++)
        {
            scanf("%d",&k);
            int w=i*z*2+j,p=i*z*2+j-z;
            if(w<=z) p=t;
            else if(w>=t) w=0;
            add(w,p,k);
        }
    for(int i=0;i<n-1;i++)  
        for(int j=1;j<=m;j++)
        {
            scanf("%d",&k);
            int w=i*z*2+z+j,p=w-m;
            if(j==1) p=0;
            else if(j==m) w=t;
            add(w,p,k);
        }
    for(int i=0;i<n-1;i++)  
        for(int j=1;j<m;j++)
        {
            scanf("%d",&k);
            int w=i*z*2+j,p=w+z;
            add(w,w+z,k);
        }
    memset(a,0x3f,sizeof(a));
    inq[0]=1; a[0]=0; q.push(0);
    while(q.size())
    {
        int x=q.front(); q.pop(); inq[x]=0;
        for(int i=head[x];i;i=nex[i])
        {
            int s=ver[i];
            if(a[s]>a[x]+edge[i]) 
            {
                a[s]=a[x]+edge[i];
                if(!inq[s]) q.push(s);
                inq[s]=1;
            }
        }
    }
    printf("%d",a[t]);
}

转载于:https://www.cnblogs.com/ZUTTER/p/10040439.html