Madgwick算法详细解读
极品巧克力
前言
接上一篇文章《Google Cardboard的九轴融合算法》。
Madgwick算法是另外一种九轴融合的方法,广泛应用在旋翼飞行器上,效果也蛮不错的。网上已经有很多madgwick算法的源代码了。
本文结合参考文献,按照我自己的理解,把Madgwick算法的来龙去脉讲清楚。
1.加权融合
由于姿态都是相对的,用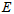 来表示水平朝北静止时的物体,
来表示水平朝北静止时的物体,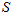 代表运动后的物体。所以,运动时的物体相对水平朝北静止时的物体的姿态可以用四元数
代表运动后的物体。所以,运动时的物体相对水平朝北静止时的物体的姿态可以用四元数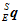 来表示。
来表示。
主要基于Madgwick算法对传感器数据进行融合。Madgwick算法的本质是加权整合t时刻的陀螺仪算出的姿态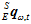 和加速度计磁场计共同算出的姿态
和加速度计磁场计共同算出的姿态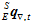 ,从而得到最终的姿态
,从而得到最终的姿态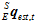 。其加权公式如下。
。其加权公式如下。
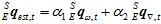
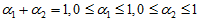
其中,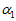 和
和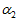 是加权系数,它们是由各自的误差占总体误差的比重所决定的,误差所占的比重越小则加权系数越大。设采样时间间隔为
是加权系数,它们是由各自的误差占总体误差的比重所决定的,误差所占的比重越小则加权系数越大。设采样时间间隔为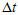 。陀螺仪的单位时间的误差
。陀螺仪的单位时间的误差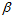 可以通过查陀螺仪的手册得到,一般是一个很小的值,所以陀螺仪的误差为
可以通过查陀螺仪的手册得到,一般是一个很小的值,所以陀螺仪的误差为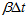 。而加速度计磁场计共同算出的姿态的误差是由计算方法决定的,计算方法如梯度下降法、高斯牛顿迭代法、牛顿法、共轭梯度法等,由于采用的方法是梯度下降法,所以其误差为梯度下降法中所选取的步长
。而加速度计磁场计共同算出的姿态的误差是由计算方法决定的,计算方法如梯度下降法、高斯牛顿迭代法、牛顿法、共轭梯度法等,由于采用的方法是梯度下降法,所以其误差为梯度下降法中所选取的步长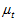 ,步长越长则其计算结果的误差越大。所以,总体误差为
,步长越长则其计算结果的误差越大。所以,总体误差为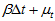 。
。
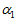 是陀螺仪算出的姿态的加权系数。
是陀螺仪算出的姿态的加权系数。
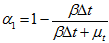
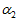 是加速度计磁场计所算出的姿态的加权系数。
是加速度计磁场计所算出的姿态的加权系数。
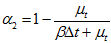
于是,接下来需要得到的是陀螺仪计算出的姿态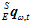 和加速度计磁场计共同算出的姿态
和加速度计磁场计共同算出的姿态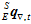 。
。
2.陀螺仪姿态估计
用陀螺仪的数据来计算出姿态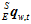 。
。
三轴陀螺仪返回的数据是自身分别绕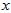 轴、
轴、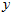 轴、
轴、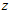 轴的角速度,这三个角速度分别用
轴的角速度,这三个角速度分别用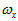 、
、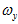 、
、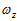 来表示。则陀螺仪返回的数据可以看成实部为零的四元数,用
来表示。则陀螺仪返回的数据可以看成实部为零的四元数,用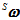 来表示。
来表示。
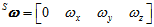
而姿态四元数变化的速度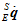 与当前的姿态
与当前的姿态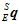 和角速度
和角速度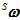 有关,其计算公式如下。
有关,其计算公式如下。
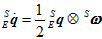
现在已知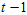 时刻的四元数
时刻的四元数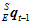 和角速度
和角速度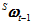 ,以及
,以及 时刻的角速度
时刻的角速度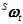 ,系统采样间隔为
,系统采样间隔为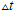 ,求
,求 时刻的四元数
时刻的四元数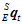 。类似于常微分方程,套用改进的欧拉公式。
。类似于常微分方程,套用改进的欧拉公式。
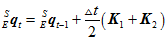
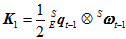





 Madgwick算法是一种用于旋翼飞行器的九轴融合方法,通过加权融合陀螺仪、加速度计和磁场计数据来估算姿态。本文深入解析算法原理,包括加权融合公式、陀螺仪姿态估计、加速度计磁场计姿态估计的梯度下降法,并探讨算法简化和磁场计修正,适合对传感器融合感兴趣的读者。
Madgwick算法是一种用于旋翼飞行器的九轴融合方法,通过加权融合陀螺仪、加速度计和磁场计数据来估算姿态。本文深入解析算法原理,包括加权融合公式、陀螺仪姿态估计、加速度计磁场计姿态估计的梯度下降法,并探讨算法简化和磁场计修正,适合对传感器融合感兴趣的读者。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章
















 2121
2121

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








