软件工程第三次作业

最新推荐文章于 2024-05-21 20:52:26 发布

weixin_30879833

最新推荐文章于 2024-05-21 20:52:26 发布

阅读量56

点赞数

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/anq312/p/10739900.html

本文深入探讨了最大连续子数组和（最大子段和）问题的解决方法，通过分治法实现，提供了详细的源代码及单元测试案例，确保算法的正确性和效率。

一、题目要求

最大连续子数组和（最大子段和）
背景

问题：给定n个整数（可能为负数）组成的序列a[1],a[2],a[3],…,a[n],求该序列如a[i]+a[i+1]+…+a[j]的子段和的最大值。当所给的整数均为负数时定义子段和为0，依此定义，所求的最优值为： Max{0,a[i]+a[i+1]+…+a[j]},1<=i<=j<=n
例如，当（a[1],a[2],a[3],a[4],a[5],a[6]）=(-2,11,-4,13,-5,-2)时，最大子段和为20。
-- 引用自<百度百科>

二、程序设计

刚看到题目时，对于此问题没有什么主要思路，参考百度百科内的分治法算法后搞懂编写。
代码coding。
源代码:

#include<stdio.h>
#include<stdlib.h>
#define MAX 100
int maxsz(int *a,int L, int R);
//int a[MAX];
int main()
{
    int i, count;
    scanf_s("%d", &count);
    for (i = 0; i < count; i++)
        scanf_s("%d", &a[i]);
    printf("%d\n", maxsz(0, count - 1));
    system("pause");
    return 0;
}
int maxsz(int *a,int L, int R)
{
    int center, i, sum, L_sum, R_sum, L_max, R_max;
    if (L == -1|| R==1)
        return 0;
    center = (L + R) >> 1;
    if (L == R)
        return a[L] > 0 ? a[L] : 0;
    else
    {
        L_sum = maxsz(a,L, center);
        R_sum = maxsz(a,center + 1, R);
        sum = 0;
        L_max = 0;
        for (i = center; i >= L; i--)
        {
            sum += a[i];
            if (sum > L_max)
                L_max = sum;
        }
        sum = 0;
        R_max = 0;
        for (i = center + 1; i <= R; i++)
        {
            sum += a[i];
            if (sum > R_max)
                R_max = sum;
        }
        sum = R_max + L_max;
        if (sum < L_sum)
            sum = L_sum;
        if (sum < R_sum)
            sum = R_sum;
    }
    return sum;
}

流程图如下

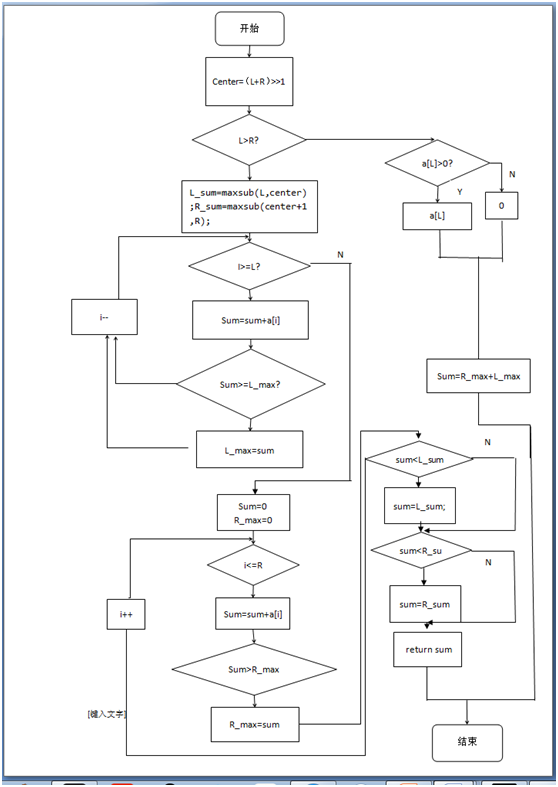
三、单元测试

选择判定/条件覆盖测试
（1）L>R
L<=R
（2）a[L]>0
a[L]<=0
（3）1>=L
1<L
（4）Sum>=L_max
Sum<L_max
（5）sum=L_sum
（6）sum=R_sum

#include "stdafx.h"
#include "CppUnitTest.h"
extern int maxsz(int *a,int left, int right);
using namespace Microsoft::VisualStudio::CppUnitTestFramework;

//extern int a[100];

namespace UnitTest1
{       
    TEST_CLASS(UnitTest1)
    {
    public:
        
        TEST_METHOD(TestMethod1)
        {
            
            int a[] = {-10,-98,-68,-45,-75,-27};
            int left = 0, right = 6;
            int sum= maxsz(a,left,right);
            Assert::AreEqual(sum,0);
        }
        TEST_METHOD(TestMethod2)
        {
            
            int *a = { };
            int left = -1, right =-1;
            int sum = maxsz(a,left, right);
            Assert::AreEqual(sum, 0);
        }
        TEST_METHOD(TestMethod3)
        {
            
            int a[] = {-6,-4,5,8,-1,4,-4,-1,-2,2,-6};
            int left = 0, right = 11;
            int sum = maxsz(a,left, right);
            Assert::AreEqual(sum,16);
        }

    };
}

测试结果显示正确