二叉树

最新推荐文章于 2025-08-15 16:44:13 发布

转载最新推荐文章于 2025-08-15 16:44:13 发布 · 44 阅读

0 ·

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/meichao/p/9237370.html

文章标签：

#数据结构与算法 #php

本文详细介绍了二叉树的基本概念、满二叉树及完全二叉树的特点，并提供了前序、中序和后序遍历的具体实现代码。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

二叉树的相关概念

1、基本概念

　　二叉树每个节点最多有两个子树的结构，通常被称为“左子树”和“右子树”。

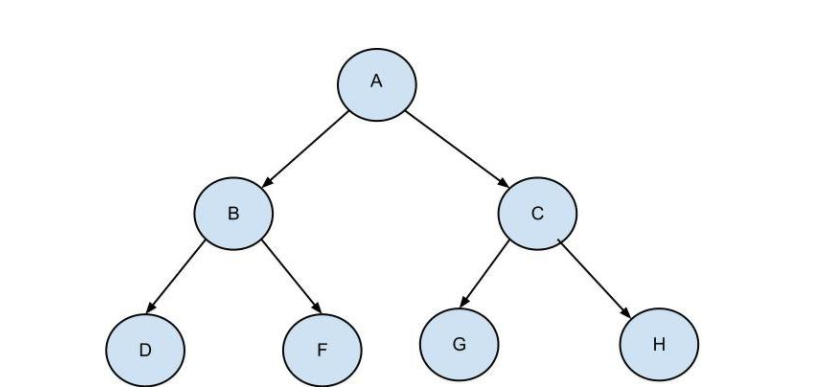
2、满二叉树

　　每个节点必须有两个子树，并且叶节点在同一层。

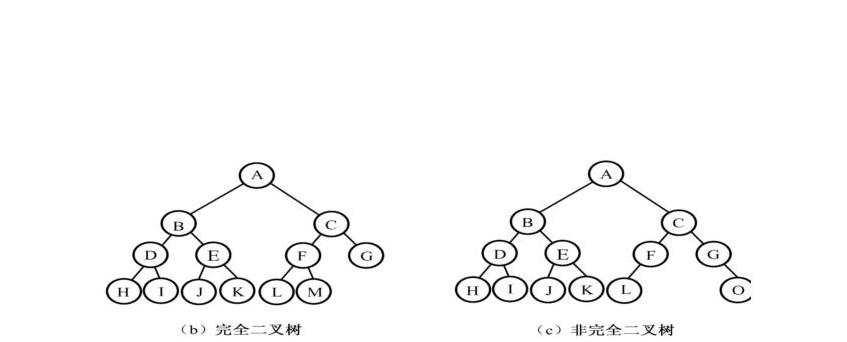
3、完全二叉树

　　节点的标记就是节点的值，意思就是节点的值是连续的，从左到右不能断裂，必须连续；

二叉树的相关遍历

1、前序遍历：根节点-》左子树-》右子树

原则：先从根节点访问到左子树的低端，然后在访问右边（每一个子树又是一个二叉树）

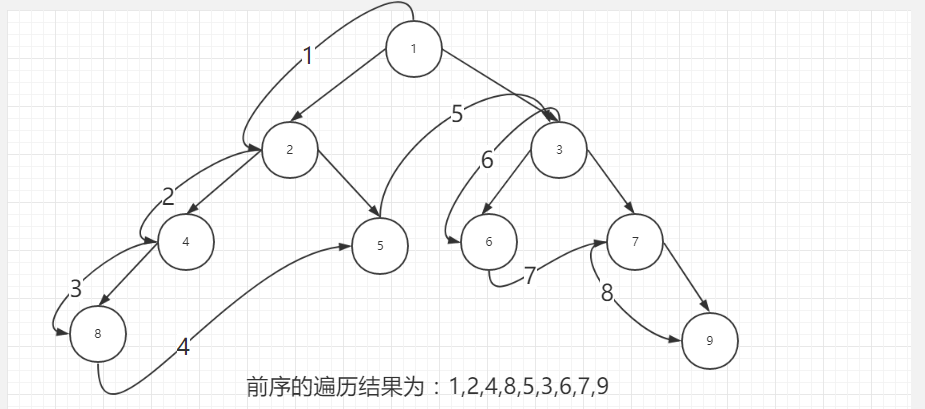
程序：

//前序遍历二叉树：根节点-》左节点-》右节点
	function preOrder($root)
	{
		$stack = [];
		array_push($stack, $root);
		while (!empty($stack)) {
			$center_node = array_pop($stack);
			echo $center_node->data.' ';
			if($center_node->right != null) array_push($stack, $center_node->right);//右子树先入栈
			if($center_node->left != null) array_push($stack, $center_node->left);
		}
	}

2、中序：根节点左子树-》根节点-》右子树

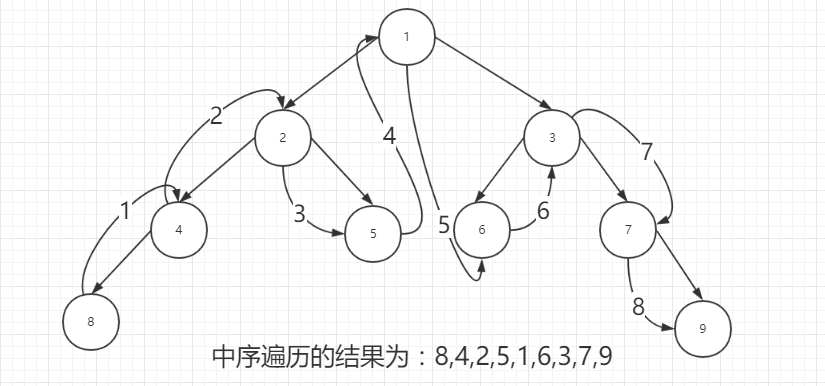
程序：

//中序遍历二叉树：左节点-》根节点-》右节点
	function mindOrder($root)
	{
		$stack = [];
		$center_node = $root;
		while(!empty($stack) || $center_node != null){
			while ($center_node != null) {
				array_push($stack, $center_node);
				$center_node = $center_node->left;
			}
			$center_node = array_pop($stack);
			echo $center_node->data.' ';
			$center_node = $center_node->right;
		}
	}

3、后序：左子树-》右子树-》根节点

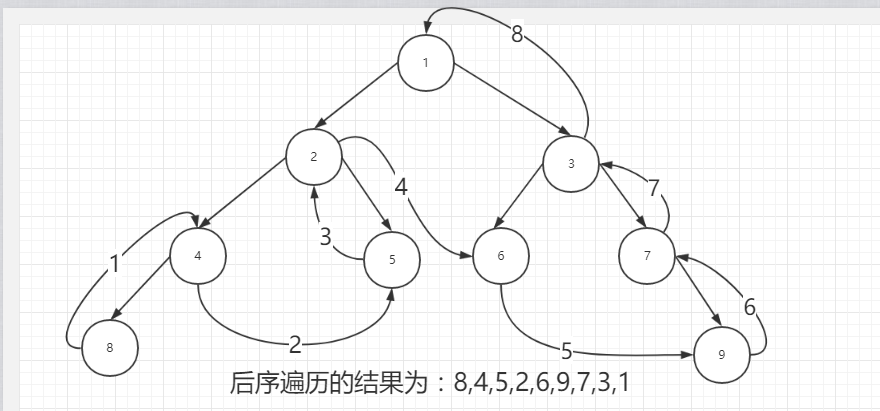
程序：

//后序遍历二叉树：左节点-》右节点-》根节点
	function afterOrder($root)
	{
		$stack = [];
		$outStack = [];
		array_push($stack, $root);
		while(!empty($stack)){
			$center_node = array_pop($stack);
			array_push($outStack, $center_node);
			if($center_node->left!=null)array_push($stack, $center_node->left);
			if($center_node->right!=null)array_push($stack, $center_node->right);
		}
		while (!empty($outStack)){
			$center_node= array_pop($outStack);
			echo $center_node->data." ";
		}

	}

完整的程序

<?php
	class Node{
		public $left;
		public $data;
		public $right;
	}
	//前序遍历二叉树：根节点-》左节点-》右节点
	function preOrder($root)
	{
		$stack = [];
		array_push($stack, $root);
		while (!empty($stack)) {
			$center_node = array_pop($stack);
			echo $center_node->data.' ';
			if($center_node->right != null) array_push($stack, $center_node->right);//右子树先入栈
			if($center_node->left != null) array_push($stack, $center_node->left);
		}
	}
	//中序遍历二叉树：左节点-》根节点-》右节点
	function mindOrder($root)
	{
		$stack = [];
		$center_node = $root;
		while(!empty($stack) || $center_node != null){
			while ($center_node != null) {
				array_push($stack, $center_node);
				$center_node = $center_node->left;
			}
			$center_node = array_pop($stack);
			echo $center_node->data.' ';
			$center_node = $center_node->right;
		}
	}
	//后序遍历二叉树：左节点-》右节点-》根节点
	function afterOrder($root)
	{
		$stack = [];
		$outStack = [];
		array_push($stack, $root);
		while(!empty($stack)){
			$center_node = array_pop($stack);
			array_push($outStack, $center_node);
			if($center_node->left!=null)array_push($stack, $center_node->left);
			if($center_node->right!=null)array_push($stack, $center_node->right);
		}
		while (!empty($outStack)){
			$center_node= array_pop($outStack);
			echo $center_node->data." ";
		}

	}
$a=new Node();  
$b=new Node();  
$c=new Node();  
$d=new Node();  
$e=new Node();  
$f=new Node();  
$h=new Node();  
$k=new Node();  
$m=new Node(); 
$a->data=1;  
$b->data=2;  
$c->data=3;  
$d->data=4;  
$e->data=5;  
$f->data=6;  
$h->data=7; 
$k->data=8; 
$m->data=9; 
$a->left=$b;  
$a->right=$c;  
$b->left=$d;  
$b->right=$e;  
$c->left=$f;  
$c->right=$h; 
$d->left = $k;
$h->right = $m; 
mindOrder($a);

转载于:https://www.cnblogs.com/meichao/p/9237370.html