多变量微积分笔记3——二元函数的极值

什么是极值

　　极值不同于最值，极值的定义如下：

　　若函数f(x)在x₀的一个邻域D有定义，且对D中除x₀的所有点，都有f(x)<f(x₀)，则称f(x₀)是函数f(x)的一个极大值。同理，若对D的所有点，都有f(x)>f(x₀)，则称f(x₀)是函数f(x)的一个极小　值。极大值和极小值也称为局部最大值和局部最小值。

　　如果用图形解释，那么：当我们在极大值点上，向任何方向移动输入点都会减小函数值；当我们在极小值点上，向任何方向移动输入点都会增加函数值。

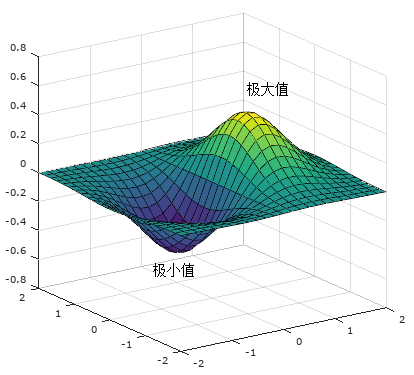
　　极值的概念来自数学应用中的最大最小值问题。根据极值定律，定义在一个有界闭区域上的每一个连续函数都必定达到它的最大值和最小值，问题在于要确定它在哪些点处达到最大值或最小值。极值点只能在函数不可导的点或导数为零的点上取得。

　　极值定律：当函数f(x)在闭区间[a,b]上是连续函数时，存在c属于[a,b]，d属于[a,b],有f(c)≤f(x)≤f(d),x∈[a,b]成立。

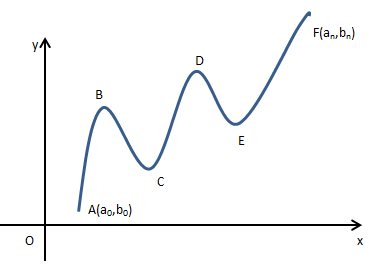
　　可以看出，极值是一个局部概念，我们可以说极大值是函数在某个区间内的最大值。一个函数可能有多个极值，如下图所示，B,C,D,E均为极值点：

　　

　　对于一元函数，求得极值和最值较为容易，但是对于多元函数，情况就复杂的多。这里主要介绍如何求解二元函数的极值（对于更多元函数的极值，在后续章节学习梯度后将继续阐述），在此之前还需要弄清楚另外两个点——临界点和鞍点。

临界点（驻点）

　　对于一个多元函数f，如果有一个点满足f所有自变量的偏导都同时为0，那么这个点被称为f的临界点，也称为驻点。