2019年春季学期第三周作业

转载于 2019-03-14 13:52:00 发布 · 60 阅读

0 ·

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/xqldc/p/10529843.html

本文探讨了如何寻找整数数组中具有最大和的子数组，通过实例解释了穷举法的实现，并反思了算法效率，同时分享了上三角矩阵判断的代码与思考过程。

本周作业

本周请大家完成上周挑战作业的第一部分：给定一个整数数组(包含正负数)，找到一个具有最大和的子数组，返回其最大的子数组的和。
例如：[1, -2, 3, 10, -4, 7, 2, -5]的最大子数组为[3, 10, -4, 7, 2]

1）.实验代码

#include<stdio.h>
#include<stdlib.h>
int main(void)
{
    FILE*fp;
    int n, i, num, s, x,sum=0,z,big,zhu, jishuqi=0;
    if((fp=fopen("E:\\lidaichuan\\ldx.txt","a+"))==NULL){
        printf("File open error!\n");
        exit(0); 
    }
    fscanf(fp,"%d", &n); 
    int a[n];
    for(i=0; i<n; i++){
        fscanf(fp,"%d，", &a[i]);
    }
    big=a[0];
    s=n;
    for(i=0; i<n; i++){
        num=i+1; 
        for(z=0; z<s; z++){
            for(x=z; x<num; x++){
                sum=sum+a[x];
                big=(big>sum)?big:sum;
            }
            sum=0;
            ++num;
        }
        s--;
    }
    fseek(fp, 0L, 1);
    fprintf(fp, "\n%d\n", big);
    s=n;
    sum=0;
    for(i=0; i<n; i++){
        num=i+1; 
        for(z=0; z<s; z++){
            for(x=z; x<num; x++){
                sum=sum+a[x];
                if(big==sum){
                    for(zhu=z; zhu<num; zhu++){
                        fprintf(fp, "%d,", a[zhu]);
                    }
                    jishuqi=10;
                }
                if(jishuqi==10){
                    break;
                }
            }
            sum=0;
            ++num;
            if(jishuqi==10){
                break;
            }
        }
        s--;
        if(jishuqi==10){
            break;
        }
    }
    if(fclose(fp)){
        printf("Can not close the file!\n");
        exit(0);
    }
    
    return 0;
 }

2)设计思路

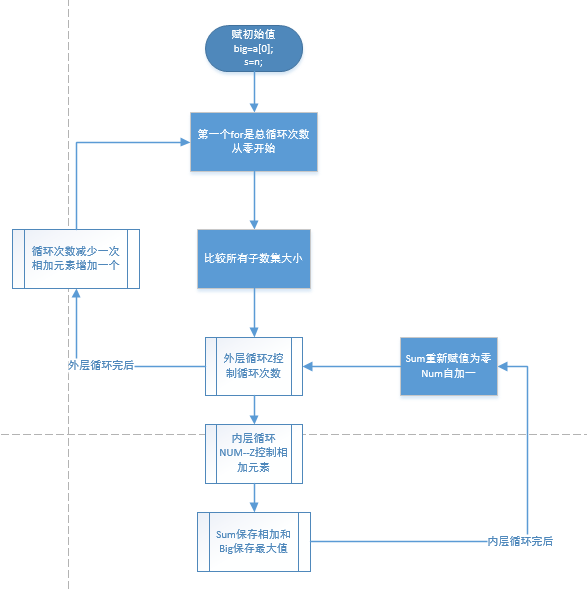
3）本题做对过程碰到问题及解决办法

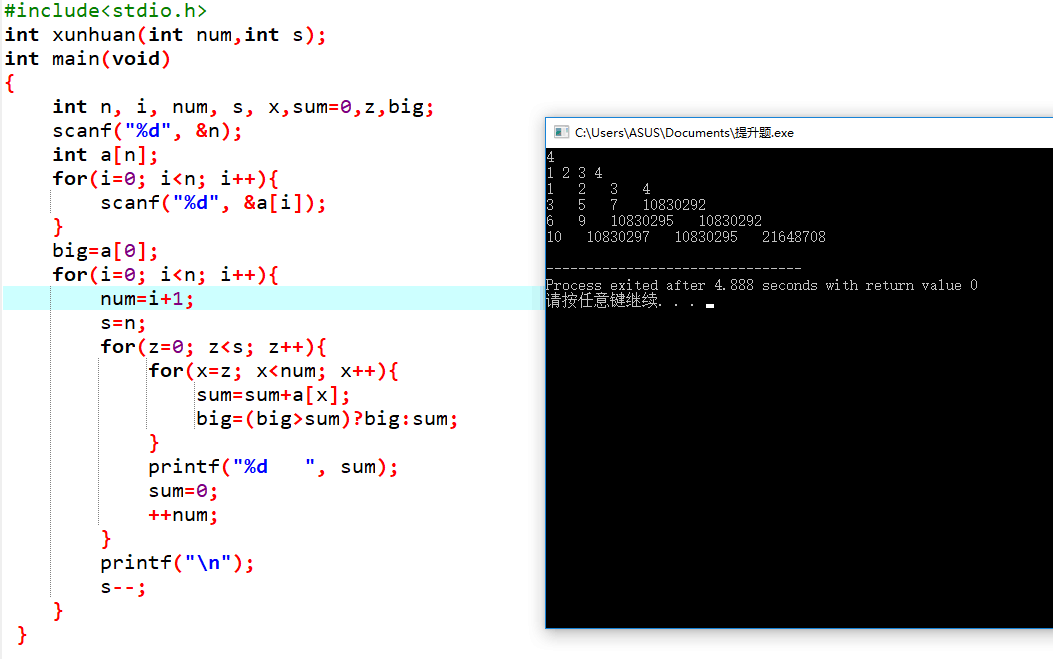
发现是，s=n；放到了第一个for循环中，这导致每一次for循环，就会使s被重新赋值。导致后面控制子数集循环时每一次都会循环n次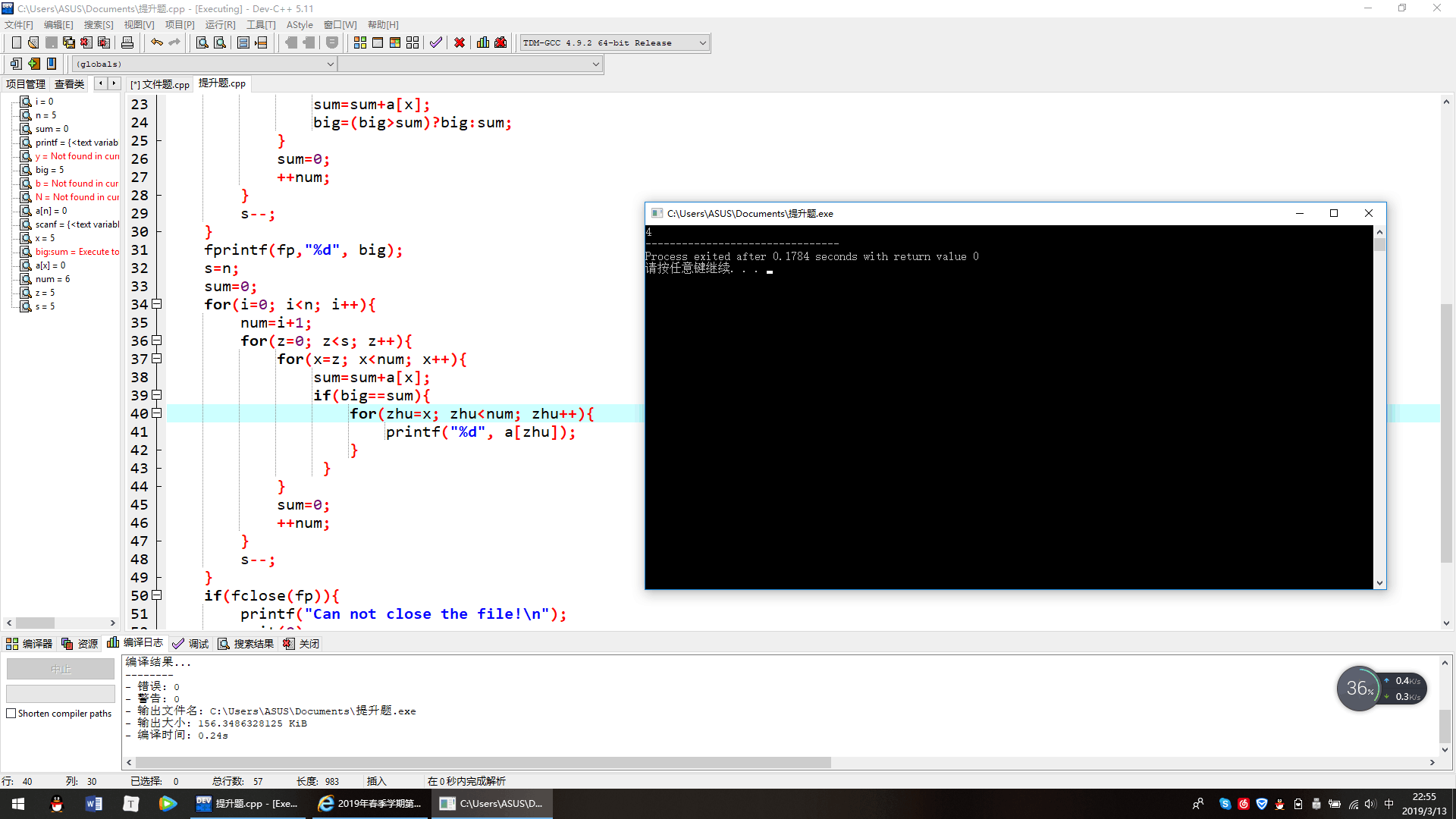

这次是写入的时候，控制输出数据的起使量赋值错误，不该是zhu=x，应该为zhu=z。

正确截图

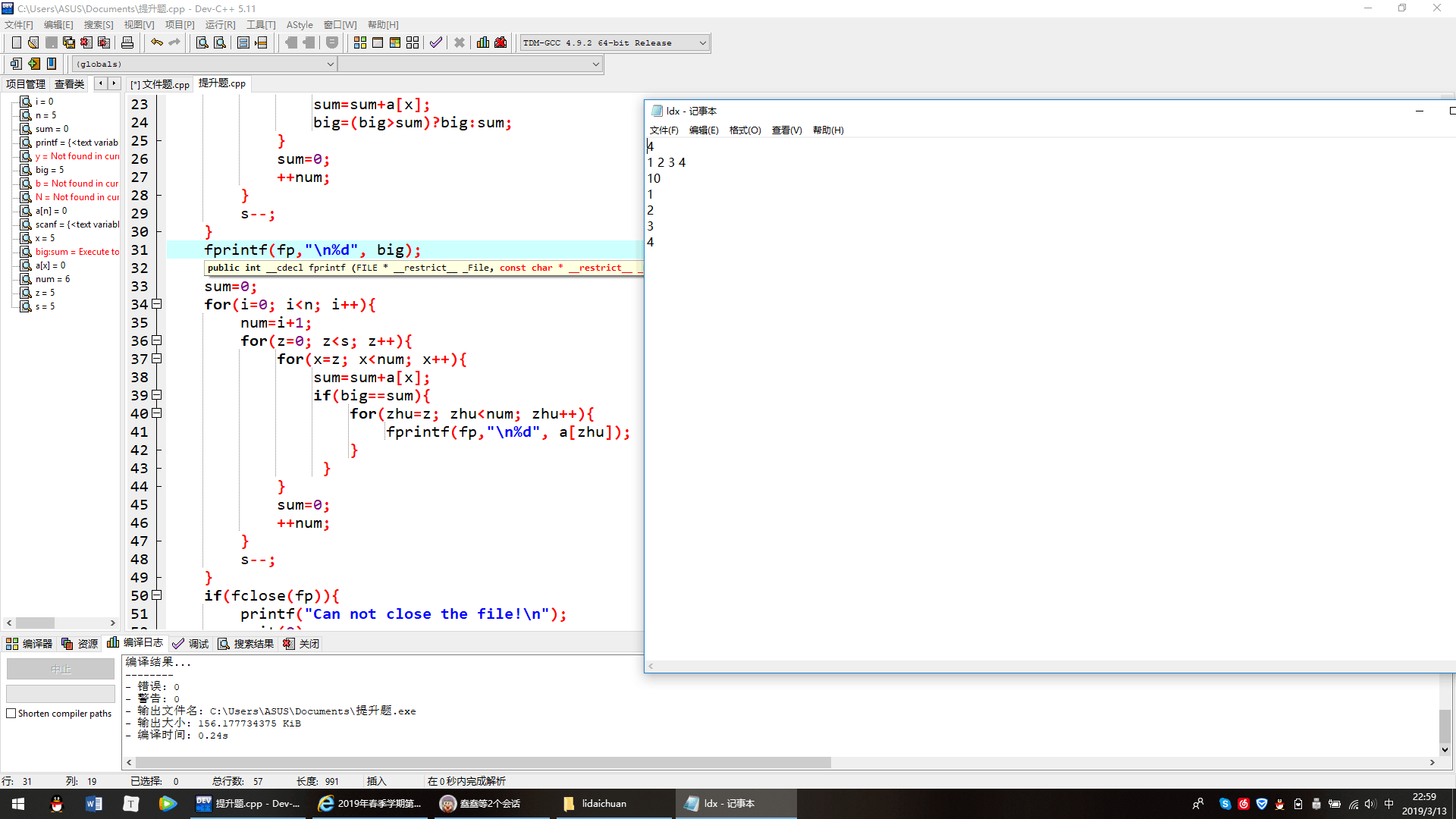
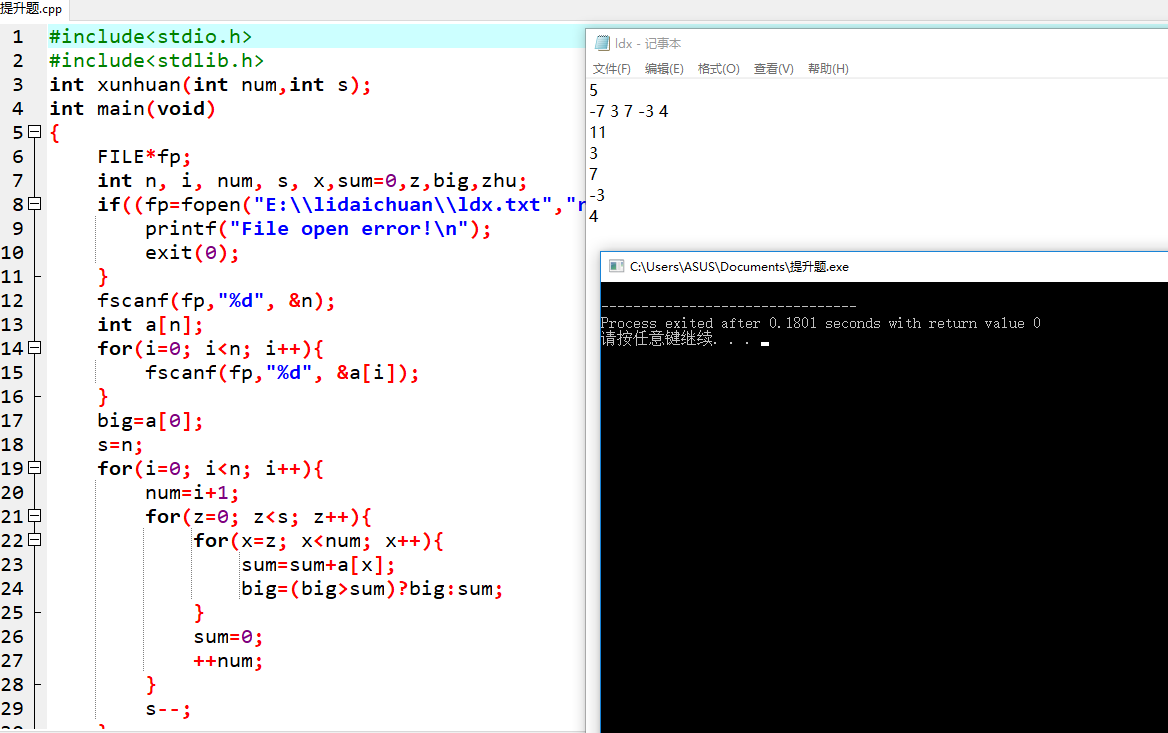
对自己作业评价

做了大概三个小时吧，感觉很好，但是穷举法运算量会不会太大？还有待改进。

学习感悟

学如逆水行舟，不进则退。这次的起点思路还是问了室友何磊才得到的。自己当时还搞错了子数集的定义，自己还是太差了，得继续努力虚心学习。

7-1 判断上三角矩阵（15 分)
上三角矩阵指主对角线以下的元素都为0的矩阵；主对角线为从矩阵的左上角至右下角的连线。
本题要求编写程序，判断一个给定的方阵是否上三角矩阵。
输入格式：
输入第一行给出一个正整数T，为待测矩阵的个数。接下来给出T个矩阵的信息：每个矩阵信息的第一行给出一个不超过10的正整数n。随后n行，每行给出n个整数，其间以空格分隔。
输出格式：
每个矩阵的判断结果占一行。如果输入的矩阵是上三角矩阵，输出“YES”，否则输出“NO”。
输入样例：
2
3
1 2 3
0 4 5
0 0 6
2
1 0
-8 2
输出样例：
YES
NO

实验代码

#include<stdio.h>
int main(void)
{
    int T,i,line,column,n,x=0;
    scanf("%d", &T);
    int b[T];
    for(i=0; i<T; i++){
        scanf("%d", &n);
        int a[n][n];
        for(line=0; line<n; line++){
            for(column=0; column<n; column++){
                scanf("%d", &a[line][column]);
            }
        }
        for(line=0; line<n; line++){
            for(column=0; column<n; column++){
                if((line>column)&&(a[line][column]!=0)){
                    b[i]=1;
                    break;
                }
            }
        }
        if(b[i]!=1){
            b[i]=0;
        }
    }
    while(x<T){
        if(b[x]==0){
            printf("YES\n");
        }
        else{
            printf("NO\n");
        }
        x++;
    }
 }

设计思路

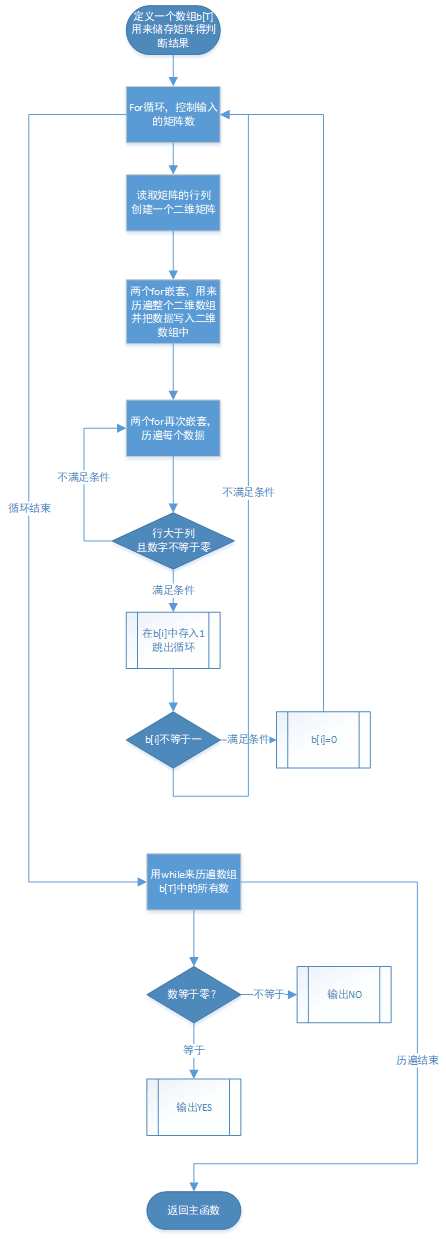
3）本题做对过程碰到问题及解决办法

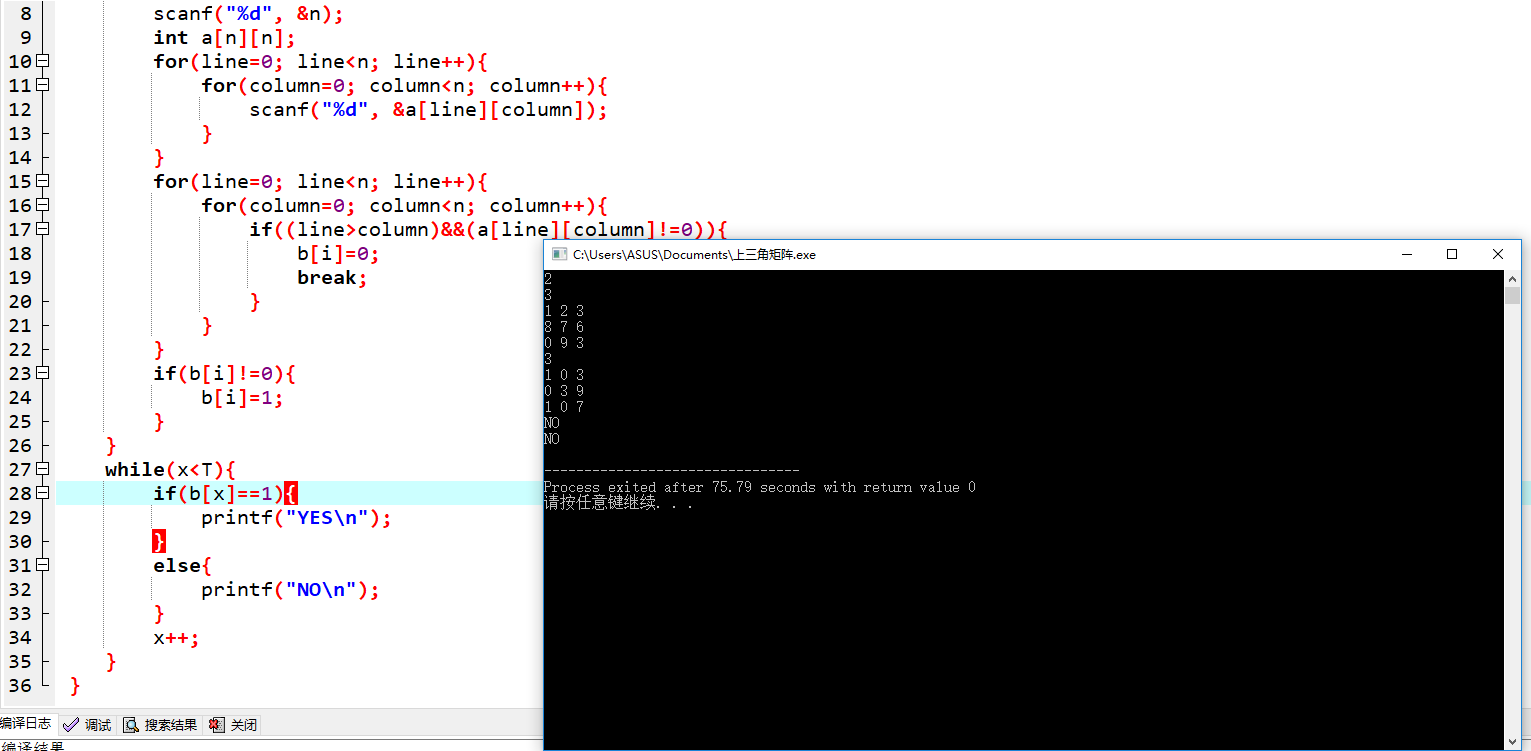
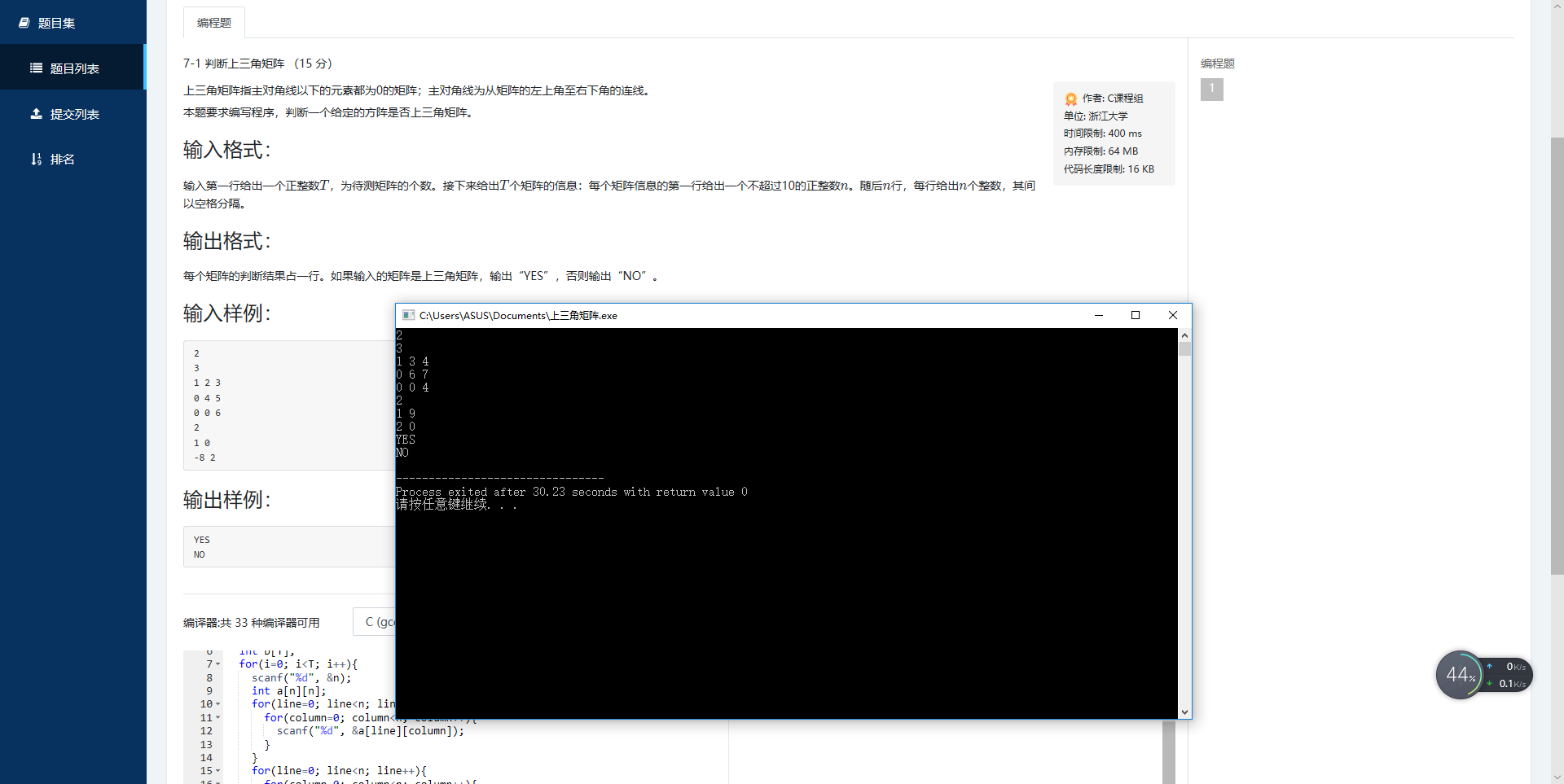
本来是一次对的，但是很让人烦恼的是：在PTA上总是不对。后来，还是李钰祺帮我改好了，能在PTA上正确了。
就改了一和零的位置，原来是矩阵的话就在b[T]里存入零，现在变成了存入一。后面的零和一的位置也置换了。
但是现在还是不明白为什么PTA会判我错，明明原来的更好呀。

正确截图

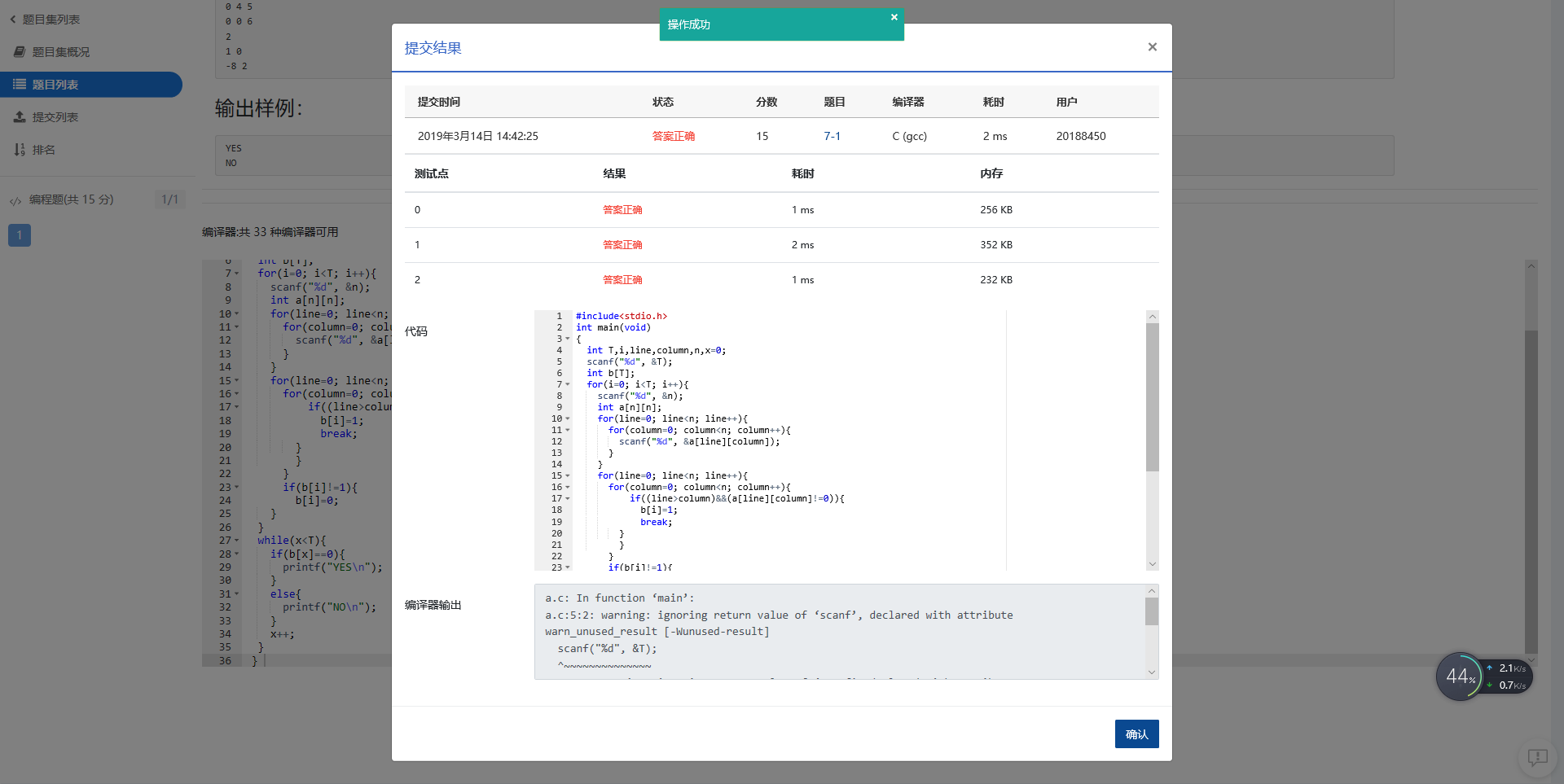
对自己作业的评价

这次作业做的应该算又快又好吧，虽然PTA上没有正确，但还可以做的更好的，加油！

学习进度条

周	这周所花的时间	代码行	学到的知识点简介	目前比较迷惑的问题
第三周	八小时	106	二维数组的基本知识	PTA的测试点是啥，第一个题除了穷举法还有没有其他方法？指针在文件中的写入位置在哪？怎么来确定的？