本文介绍了两道经典算法题目，分别是“狼抓兔子”和“海拔”问题，并详细解析了如何利用平面图最小割转化为最短路径问题的方法来解决这两道题目。
最近做了一下這兩題，所以做個簡單的總結。
1001: [BeiJing2006]狼抓兔子
Time Limit: 15 Sec Memory Limit: 162 MBSubmit: 5710 Solved: 1290
[ Submit][ Status][ Discuss]
Description
现在小朋友们最喜欢的"喜羊羊与灰太狼",话说灰太狼抓羊不到，但抓兔子还是比较在行的，而且现在的兔子还比较笨，它们只有两个窝，现在你做为狼王，面对下面这样一个网格的地形：
左上角点为(1,1),右下角点为(N,M)(上图中N=4,M=5).有以下三种类型的道路 1:(x,y)<==>(x+1,y) 2:(x,y)<==>(x,y+1) 3:(x,y)<==>(x+1,y+1) 道路上的权值表示这条路上最多能够通过的兔子数，道路是无向的. 左上角和右下角为兔子的两个窝，开始时所有的兔子都聚集在左上角(1,1)的窝里，现在它们要跑到右下解(N,M)的窝中去，狼王开始伏击这些兔子.当然为了保险起见，如果一条道路上最多通过的兔子数为K，狼王需要安排同样数量的K只狼，才能完全封锁这条道路，你需要帮助狼王安排一个伏击方案，使得在将兔子一网打尽的前提下，参与的狼的数量要最小。因为狼还要去找喜羊羊麻烦.
左上角点为(1,1),右下角点为(N,M)(上图中N=4,M=5).有以下三种类型的道路 1:(x,y)<==>(x+1,y) 2:(x,y)<==>(x,y+1) 3:(x,y)<==>(x+1,y+1) 道路上的权值表示这条路上最多能够通过的兔子数，道路是无向的. 左上角和右下角为兔子的两个窝，开始时所有的兔子都聚集在左上角(1,1)的窝里，现在它们要跑到右下解(N,M)的窝中去，狼王开始伏击这些兔子.当然为了保险起见，如果一条道路上最多通过的兔子数为K，狼王需要安排同样数量的K只狼，才能完全封锁这条道路，你需要帮助狼王安排一个伏击方案，使得在将兔子一网打尽的前提下，参与的狼的数量要最小。因为狼还要去找喜羊羊麻烦.
Input
第一行为N,M.表示网格的大小，N,M均小于等于1000.接下来分三部分 第一部分共N行，每行M-1个数，表示横向道路的权值. 第二部分共N-1行，每行M个数，表示纵向道路的权值. 第三部分共N-1行，每行M-1个数，表示斜向道路的权值. 输入文件保证不超过10M
Output
输出一个整数，表示参与伏击的狼的最小数量.
Sample Input
3 4
5 6 4
4 3 1
7 5 3
5 6 7 8
8 7 6 5
5 5 5
6 6 6
5 6 4
4 3 1
7 5 3
5 6 7 8
8 7 6 5
5 5 5
6 6 6
Sample Output
14
分析：很顯然，我們可以直接構造出圖然後跑一次最大流求出最小割。但是時限不夠。。。
所以我們可以構造一個最短路的模型來做，具體看論文 平面圖求最小割
以下是建的最短路模型的圖：從圖中我們可以看出，我們求S到T的最短路即為最小割，因為沿著最短路經過的路徑與原圖相交的邊即為割邊。
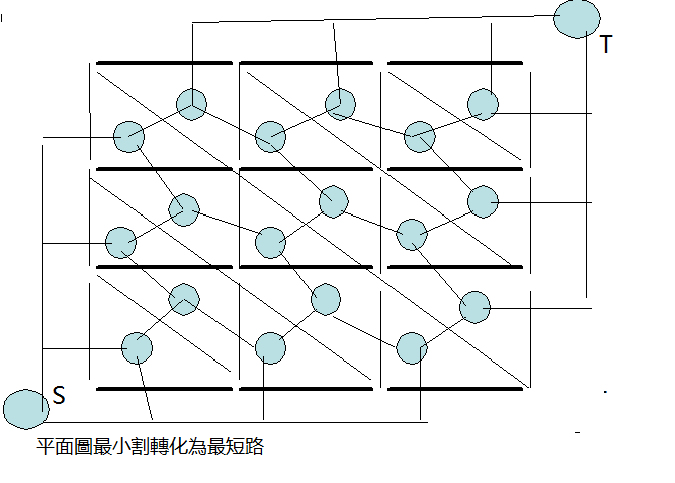
所以我們可以按照上圖直接構造出無向圖，直接跑一次堆優化的dijkstra或者spfa即可求出答案。
代碼：
/*
* 分析：
* 平面图最小割转化为最短路问题。
* */
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <queue>
using namespace std;
const int X = 1000002*2;
const int inf = 1e9;
#define debug puts("here");
int id[2][1001][1001];
struct node{
int y,dis,next;
}edge[X*6];
int ds,dt,tot;
int n,m;
int dis[X];
int po[X],tol;
void add(int x,int y,int w){
edge[++tol].y = y;
edge[tol].dis = w;
edge[tol].next = po[x];
po[x] = tol;
edge[++tol].y = x;
edge[tol].dis = w;
edge[tol].next = po[y];
po[y] = tol;
}
void build(){
tot = 0;
for(int j=1;j<n;j++)
for(int k=1;k<m;k++)
for(int i=0;i<2;i++)
id[i][j][k] = ++tot;
ds = ++ tot;
dt = ++ tot;
memset(po,0,sizeof(po));
tol = 0;
int w;
int ok = 0;
int check = n*(m-1)+(n-1)*m+(n-1)*(m-1);
/*********** 1 ******************/
for(int i=1;i<m;i++){
scanf("%d",&w);
ok ++;
add(id[1][1][i],dt,w);
}
for(int i=2;i<n;i++){
for(int j=1;j<m;j++){
scanf("%d",&w);
ok ++;
add(id[0][i-1][j],id[1][i][j],w);
}
}
for(int i=1;i<m;i++){
scanf("%d",&w);
add(ds,id[0][n-1][i],w);
ok ++;
}
/*********** 1 ******************/
/*********** 2 ******************/
for(int i=1;i<n;i++){
for(int j=1;j<=m;j++){
scanf("%d",&w);
ok ++;
if(j==1)
add(ds,id[0][i][1],w);
else if(j==m)
add(id[1][i][m-1],dt,w);
else
add(id[0][i][j],id[1][i][j-1],w);
}
}
/*********** 2 ******************/
for(int i=1;i<n;i++){
for(int j=1;j<m;j++){
if(ok>=check)
debug;
scanf("%d",&w);
add(id[1][i][j],id[0][i][j],w);
ok ++;
}
}
}
struct state{
int x,w;
state(){}
state(int _x,int _w):x(_x),w(_w){}
friend bool operator < (state a,state b){
return a.w > b.w;
}
};
priority_queue<state> q;
int dijkstra(){
while(q.size())
q.pop();
for(int i=1;i<=tot;i++)
dis[i] = inf;
dis[ds] = 0;
q.push(state(ds,0));
while(q.size()){
state tmp = q.top();;
q.pop();
int x = tmp.x;
if(tmp.w>dis[x])
continue;
if(x==dt)
return tmp.w;
for(int i=po[x];i;i=edge[i].next){
int y = edge[i].y;
int cur = dis[x]+edge[i].dis;
if(cur < dis[y]){
dis[y] = cur;
q.push(state(y,cur));
}
}
}
return -1;
}
int main(){
while(cin>>n>>m){
if(n==1||m==1){
int ans = inf;
int x;
for(int i=1;i<max(n,m);i++){
scanf("%d",&x);
ans = min(ans,x);
}
cout<<ans<<endl;
continue;
}
build();
cout<<dijkstra()<<endl;
}
return 0;
}
2007: [Noi2010]海拔
Time Limit: 20 Sec Memory Limit: 552 MBSubmit: 778 Solved: 332
[ Submit][ Status][ Discuss]
Description
YT市是一个规划良好的城市，城市被东西向和南北向的主干道划分为n×n个区域。简单起见，可以将YT市看作一个正方形，每一个区域也可看作一个正方形。从而，YT城市中包括(n+1)×(n+1)个交叉路口和2n×(n+1)条双向道路（简称道路），每条双向道路连接主干道上两个相邻的交叉路口。下图为一张YT市的地图(n = 2)，城市被划分为2×2个区域，包括3×3个交叉路口和12条双向道路。 小Z作为该市的市长，他根据统计信息得到了每天上班高峰期间YT市每条道路两个方向的人流量，即在高峰期间沿着该方向通过这条道路的人数。每一个交叉路口都有不同的海拔高度值，YT市市民认为爬坡是一件非常累的事情，每向上爬h的高度，就需要消耗h的体力。如果是下坡的话，则不需要耗费体力。因此如果一段道路的终点海拔减去起点海拔的值为h(注意h可能是负数)，那么一个人经过这段路所消耗的体力是max{0, h}（这里max{a, b}表示取a, b两个值中的较大值）。 小Z还测量得到这个城市西北角的交叉路口海拔为0，东南角的交叉路口海拔为1(如上图所示)，但其它交叉路口的海拔高度都无法得知。小Z想知道在最理想的情况下（即你可以任意假设其他路口的海拔高度），每天上班高峰期间所有人爬坡所消耗的总体力和的最小值。
Input
第一行包含一个整数n，含义如上文所示。 接下来4n(n + 1)行，每行包含一个非负整数分别表示每一条道路每一个方向的人流量信息。输入顺序：n(n + 1)个数表示所有从西到东方向的人流量，然后n(n + 1)个数表示所有从北到南方向的人流量，n(n + 1)个数表示所有从东到西方向的人流量，最后是n(n + 1)个数表示所有从南到北方向的人流量。对于每一个方向，输入顺序按照起点由北向南，若南北方向相同时由西到东的顺序给出(参见样例输入)。
Output
仅包含一个数，表示在最理想情况下每天上班高峰期间所有人爬坡所消耗的总体力和（即总体力和的最小值），结果四舍五入到整数。
Sample Input
1
1
2
3
4
5
6
7
8
1
2
3
4
5
6
7
8
Sample Output
3
【样例说明】
样例数据见下图。
最理想情况下所有点的海拔如上图所示。
【数据规模】
对于20%的数据：n ≤ 3；
对于50%的数据：n ≤ 15；
对于80%的数据：n ≤ 40；
对于100%的数据：1 ≤ n ≤ 500，0 ≤ 流量 ≤ 1,000,000且所有流量均为整数。
【样例说明】
样例数据见下图。
最理想情况下所有点的海拔如上图所示。
【数据规模】
对于20%的数据：n ≤ 3；
对于50%的数据：n ≤ 15；
对于80%的数据：n ≤ 40；
对于100%的数据：1 ≤ n ≤ 500，0 ≤ 流量 ≤ 1,000,000且所有流量均为整数。
分析：
我們可以證明，圖中只會存在海拔為0和1的兩種高度，並且0、1分別為一個聯通塊。
所以我們要求的最小值就是如何把0,1分開成兩個聯通塊，並且使得從0到1的人數和值最小。
所以可以轉化為求原圖的平面圖的最小割。
對於這題，其實跟上面的那題基本一樣。但是這裡是雙向的邊。。。
所以我們可以這樣建圖：注意從低到高消耗體力。
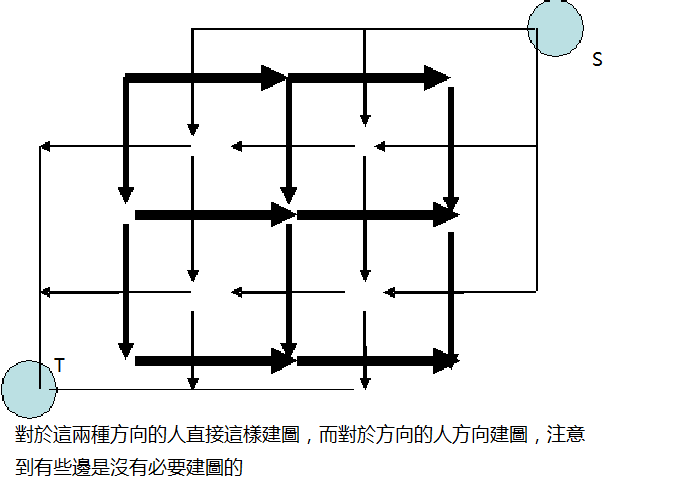
同樣的，附上代碼
/*
分析：平面圖最小割轉化為最短路。
*/
#include <set>
#include <map>
#include <cmath>
#include <queue>
#include <stack>
#include <string>
#include <vector>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
#define lx(x) (x<<1)
#define rx(x) (x<<1|1)
#define debug puts("here")
#define rep(i,n) for(int i=0;i<n;i++)
#define rep1(i,n) for(int i=1;i<=n;i++)
#define REP(i,a,b) for(int i=a;i<=b;i++)
#define foreach(i,vec) for(unsigned i=0;i<vec.size();i++)
#define pb push_back
#define RD(n) scanf("%d",&n)
#define RD2(x,y) scanf("%d%d",&x,&y)
#define RD3(x,y,z) scanf("%d%d%d",&x,&y,&z)
#define RD4(x,y,z,w) scanf("%d%d%d%d",&x,&y,&z,&w)
/******** program ********************/
const int MAXN = 505*505;
const int MAXM = MAXN*16;
int po[MAXN],tol,n,m,s,t;
int dis[MAXN];
bool use[MAXN];
struct Edge{
int y,val,next;
}edge[MAXM];
struct node{
int x;
int val;
node(){}
node(int _x,int _val):x(_x),val(_val){}
friend bool operator < (node a,node b){
return a.x>b.x;
}
};
priority_queue<node> q;
void add(int x,int y,int val){
edge[++tol].y = y;
edge[tol].val = val;
edge[tol].next = po[x];
po[x] = tol;
}
int dijkstra(){
memset(dis,0x7f,sizeof(dis));
q.push(node(s,0));
dis[s] = 0;
while(q.size()){
node p = q.top();
q.pop();
int x = p.x;
if(p.val>dis[x]) // 小優化
continue;
if(x==t)
return p.val;
for(int i=po[x];i;i=edge[i].next){
int y = edge[i].y;
int cur = edge[i].val+dis[x];
if(cur<dis[y]){
dis[y] = cur;
q.push( node(y,cur) );
}
}
}
while(true)
;
return -1;
}
int id(int x,int y){
return x*n-n+y;
}
void init(){
RD(n);
int val;
s = n*n+1;
t = s+1;
/******************************************/
rep1(i,n){
RD(val);
add( s,id(1,i),val );
}
rep1(i,n-1){
rep1(j,n){
RD(val);
add( id(i,j),id(i+1,j),val );
}
}
rep1(i,n){
RD(val);
add( id(n,i),t,val );
}
/******************************************/
rep1(i,n){
RD(val);
add( id(i,1),t,val );
rep1(j,n-1){
RD(val);
add( id(i,j+1),id(i,j),val );
}
RD(val);
add( s,id(i,n),val );
}
/******************************************/
rep1(i,n) RD(val); // 這樣的邊沒有意義
rep1(i,n-1){
rep1(j,n){
RD(val);
add( id(i+1,j),id(i,j),val );
}
}
rep1(i,n) RD(val);
/******************************************/
rep1(i,n){
RD(val);
rep1(j,n-1){
RD(val);
add( id(i,j),id(i,j+1),val );
}
RD(val);
}
}
int spfa(){
memset(dis,0x7f,sizeof(dis));
memset(use,false,sizeof(use));
queue<int> q;
q.push(s);
dis[s] = 0;
while(q.size()){
int x = q.front();
q.pop();
use[x] = false;
for(int i=po[x];i;i=edge[i].next){
int y = edge[i].y;
int tmp = edge[i].val+dis[x];
if(tmp<dis[y]){
dis[y] = tmp;
if(!use[y]){
use[y] = true;
q.push(y);
}
}
}
}
return dis[t];
}
int main(){
#ifndef ONLINE_JUDGE
freopen("sum.in","r",stdin);
//freopen("sum.out","w",stdout);
#endif
init();
//cout<<dijkstra()<<endl; // 堆優化的dijkstra
cout<<spfa()<<endl; // spfa
return 0;
}
扫一扫
911
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
