软件工程第三次作业

最大子段和问题

---

问题： 给定n个整数（可能为负数）组成的序列a[1],a[2],a[3],…,a[n],求该序列如a[i]+a[i+1]+…+a[j]的子段和的最大值。当所给的整数均为负数时定义子段和为0，依此定义，所求的最优值为： Max{0,a[i]+a[i+1]+…+a[j]},1<=i<=j<=n
例如，当（a[1],a[2],a[3],a[4],a[5],a[6]）=(-2,11,-4,13,-5,-2)时，最大子段和为20。
-- 引用自《百度百科》

1. 分析

• 暴力法
  我们很容易想到，枚举子区间的左端点和右端点L和R，然后从L遍历到R求和。假设我们要处理的序列长度为N，显然，这种算法的时间复杂度是O（N^3），空间复杂度为O（1）。如果数据规模较大，这种算法无法满足需求。
• 前缀和优化
  根据前一种方法，我们可以对求和部分进行优化，预处理出前缀和，可以在O（1）的时间复杂度完成求和操作，但需要额外开辟一段存储前缀和的空间。优化过后的算法时间复杂度是O（N^2），空间复杂度为O（N）。对于小规模的数据来说也许足够，但我们可以采取下边这种更加优秀的算法。
• 动态规划
  定义dp[i]为右端点为i的最大子段和，于是我们很容易得出一个递推式dp[i] = max(dp[i - 1], 0) + arr[i]。然后，我们取ans = max{dp[i]}即为所求。最后，我们发现递推过程中其实只需要维护前一个dp值即可，于是可以把空间复杂度降至O（1）。这种算法的时间复杂度是O（N），空间复杂度为O（1），是已知的针对最大字段和的效率最高的算法。

2. 流程图

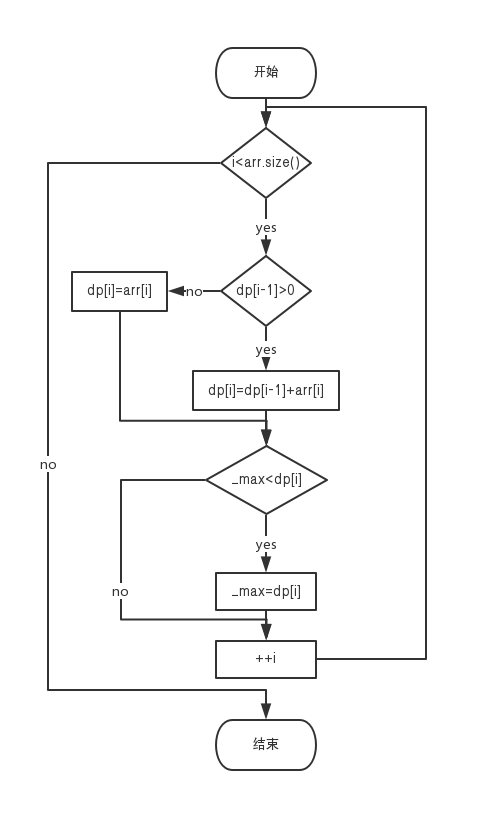
3. 源代码

Coding传送门

int Solve_3(vector<int> & arr)
{
    int dp = 0;
    int _max = 0;
    for (int i = 0; i < arr.size(); ++i) {
        dp = max(dp, 0) + arr.at(i);
        _max = max(_max, dp);
    }
    return _max;
}

运行结果如下：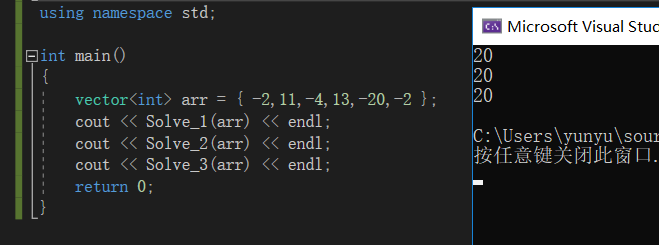

4.单元测试

条件组合覆盖

条件① : dp[i - 1] > 0 | dp[i - 1] <= 0
条件② : _max < dp[i] | _max >= dp[i]
条件组合① : dp[i - 1] > 0 && _max < dp[i]
条件组合② : dp[i - 1] > 0 && _max >= dp[i]
条件组合③ : dp[i - 1] <= 0 && _max < dp[i]
条件组合④ : dp[i - 1] <= 0 && _max >= dp[i]

当（a1,a[2],a[3],a[4],a[5],a[6]）=(-2,11,-4,13,-20,-2) 时，一组测试足以覆盖以上四个条件组合。
测试代码如下：

#include "pch.h"
#include "CppUnitTest.h"
#include "../Max/mq.h"
using namespace Microsoft::VisualStudio::CppUnitTestFramework;

namespace UnitTest
{
    TEST_CLASS(UnitTest)
    {
    public:
        
        TEST_METHOD(TestMethod1)
        {
            vector<int> arr = { -2,11,-4,13,-20,-2 };
            Assert::AreEqual(Solve_3(arr), 20);
        }
    };
}

测试结果如下：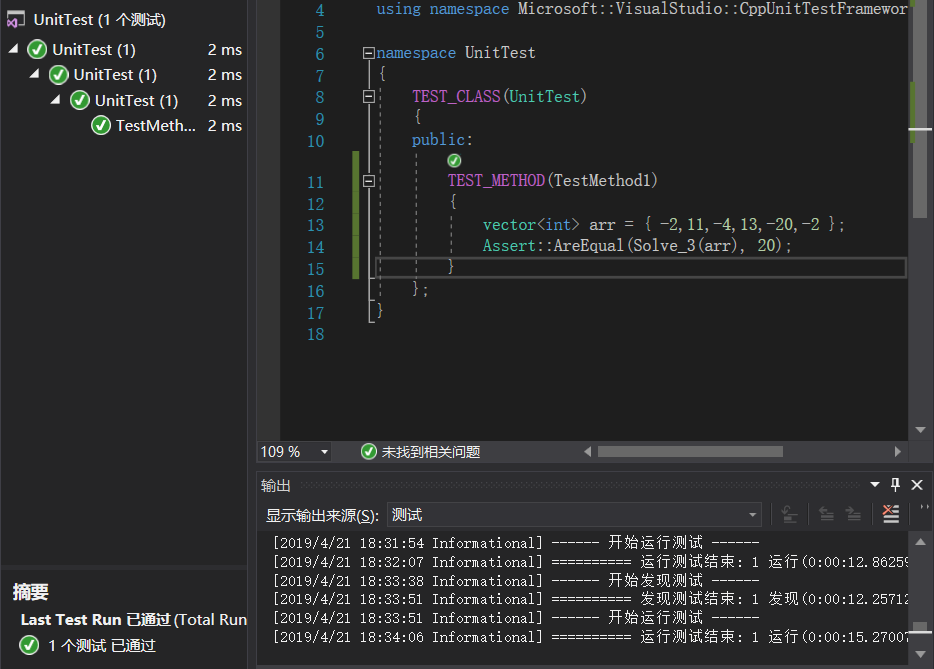

author@miaoqi
2019 年 04 月 21日

转载于:https://www.cnblogs.com/miaoqi2019/p/10745183.html