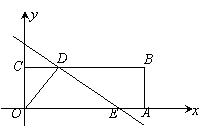
一、(2010广东广州)如图所示,四边形OABC是矩形,点A、C的坐标分别为(3,0),(0,1),点D是线段BC上的动点(与端点B、C不重合),过点D作直线y=![]() +b折线OAB于点E.
+b折线OAB于点E.
(1)记△ODE的面积为S,求S与b函数关系式;
(2)当点E在线段OA上时,若矩形OABC关于直线DE的对称图形为四边形OA1B1C1,试探究OA1B1C1与矩形OABC的重叠部分的面积是否发生变化,若不变,求出该重叠部分的面积;若改变,请说明理由.
二、已知反比例函数y=(m-8)/x(m为常数)的图象经过点A(-1,6).
(1)求m的值;
(2)如图9,过点A作直线AC与函数y=(m-8)/x的图象交于点B,与x轴交于点C,且AB=2BC,求点C的坐标.
三、(2010年广州市中考试题)已知:如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°.点E是DC的中点,过点E作DC的垂线交AB于点P,交CB的延长线于点M.点F在线段ME上,且满足CF=AD,MF=MA.
(1)若∠MFC=120°,求证:AM=2MB;
(2)求证:∠MPB=90°- ∠FCM.
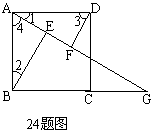
四、如图,四边形ABCD是边长为2的正方形,点G是BC延长线上一点,连结AG,点E、F分别在AG上,连接BE、DF,∠1=∠2 , ∠3=∠4.
(1)证明:△ABE≌△DAF;
(2)若∠AGB=30°,求EF的长.
五、如图,![]() 、
、 ![]() 是等腰直角三角形,点
是等腰直角三角形,点![]() 、
、![]() 在函数
在函数![]() 的图象上,斜边
的图象上,斜边![]() 、
、![]() 都在
都在![]() 轴上,则点
轴上,则点![]() 的坐标是____________.
的坐标是____________.
![clip_image002[5]](https://i-blog.csdnimg.cn/blog_migrate/49d8613bcfa194896b0db1d91f465cd0.gif)
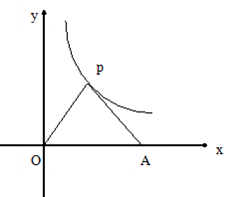
六、已知点P(m,n)(m﹥0)在反比例函数![]() 上,连OP,作PA⊥OP,交x轴于A点,A点坐标为(a,o)(a>m);
上,连OP,作PA⊥OP,交x轴于A点,A点坐标为(a,o)(a>m);![]()
(1)当n=1时,求P点坐标;
(2)当PA=OP,求k的大小;
七、如图,等腰Rt△ABC的斜边BC在 x轴上,顶点A在反比例函数x>0(3)的图像上,连接OA,则OC2-OA2=________.
八、顶点在矩形边上的菱形叫做矩形的内接菱形.
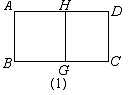
如图,矩形ABCD中,已知:![]() ,
,![]() (a<b),(1)、(2)、(3)是三种不同内接菱形的方式.
(a<b),(1)、(2)、(3)是三种不同内接菱形的方式.
①图(1)中,若AH=BG=AB,则四边形ABGH是矩形ABCD的内接菱形;
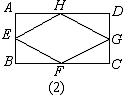
②图(2)中,若点E、F、G和H分别是AB、BC、CD和DE的中点,则四边形EFGH是矩形ABCD的内接菱形;
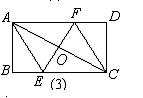
③图(3)中,若EF垂直平分对角线AC,交BC于点E,交AD于点F,交AC于点O,则四边形AECF是矩形ABCD的内接菱形.
(1)请你结合图(2)对②中的命题进行证明;
(2)试比较(1)、(2)、(3)中的矩形ABCD的三个不同内接菱形面积的面积大小并说明理由;
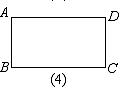
(3)在矩形ABCD中,你还能画出第4种矩形内接菱形吗?若能,请在(4)中画出;若不能,
则说明理由.
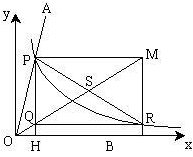
九、(2005•佛山)“三等分角”是数学史上一个著名的问题,但仅用尺规不可能“三等分角”.下面是数学家帕普斯借助函数给出的一种“三等分锐角”的方法(如图):将给定的锐角∠AOB置于直角坐标系中,边OB在x轴上、边OA与函数y= 1/x的图象交于点P,以P为圆心、以2OP为半径作弧交图象于点R.分别过点P和R作x轴和y轴的平行线,两直线相交于点M,连接OM得到∠MOB,则∠MOB= 1/3∠AOB.要明白帕普斯的方法,请研究以下问题:
(1)设P(a, 1/a)、R(b, 1/b),求直线OM对应的函数表达式(用含a,b的代数式表示);
(2)分别过点P和R作y轴和x轴的平行线,两直线相交于点Q.请说明Q点在直线OM上,并据此证明∠MOB= 1/3∠AOB;
(3)应用上述方法得到的结论,你如何三等分一个钝角(用文字简要说明).







![clip_image004[5]](https://i-blog.csdnimg.cn/blog_migrate/ea03f62517841585ac6dff2925aed840.gif)
![clip_image002[9]](https://i-blog.csdnimg.cn/blog_migrate/7b2a6a99d2ca12a2752ae06c36cf3cba.gif)
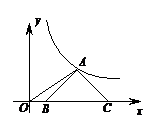
















 2087
2087

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








