codeforces C. Ilya and Matrix 解题报告-优快云博客

本文介绍了一个算法问题：如何通过排列给定的4n个整数形成2n×2n矩阵，并求得该矩阵的最大美度。美度定义为：当矩阵规模缩小时，其值等于当前最大值加上四个子矩阵的美度之和。文章给出了具体的实现代码。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题目链接：http://codeforces.com/problemset/problem/313/C

题目意思：给定 4ⁿ个整数（可以组成 2ⁿ × 2ⁿ大小的矩阵），问通过对这些整数进行排列，求出 the resulting maximum beauty of the matrix。这个最大值的定义是这样的：先定义m为所有整数中的最大值。如果n = 0，那么，这个beauty 数就是m；否则把2ⁿ × 2ⁿ大小的矩阵划分为 2^n - 1 × 2^n - 1- 大小的子矩阵，那么 beauty 数是：m + 其余4个子矩阵的beauty数。

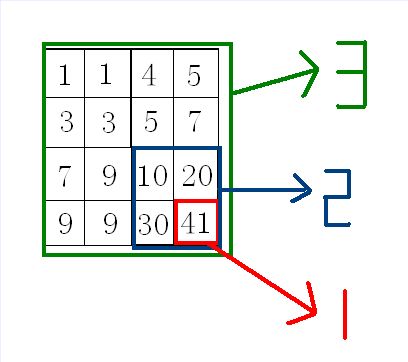
举个例子吧，假设输入的 4ⁿ 为16，16个整数为： 1 3 5 9 9 20 3 7 41 30 1 4 5 10 9 7。先排序，然后可以抽象成这样解决：（数字表示第几步要相加的和）

 1 #include <iostream>
 2 #include <cstdio>
 3 #include <cstdlib>
 4 #include <algorithm>
 5 using namespace std;
 6 
 7 const int maxn = 2*1e6 + 10;
 8 int matrix[maxn];
 9 
10 int main()
11 {
12     int i, j, n;
13     __int64 ans, sum;
14     while (scanf("%d", &n) != EOF)
15     {
16         for (i = 1; i <= n; i++)
17             scanf("%d", &matrix[i]);
18         sort(matrix+1, matrix+1+n);
19         ans = sum = 0;
20         for (j=i=1; i <= n; j <<= 2)
21         {
22             for ( ; i <= j; i++)  // 就是图中的1，2，3
23                 sum += matrix[n-i+1];
24             ans += sum;
25         }
26         printf("%I64d\n", ans);
27     }
28     return 0;
29 }