线性模型（2）：Linear Regression

此笔记源于台湾大学林轩田老师《机器学习基石》《机器学习技法》

 

我们已经学习过PLA算法，所谓的线性模型就是：计算核心为。PLA是一种分类方法，这里介绍线性回归方法（与概率与统计中的线性回归相同）。

令，则有：

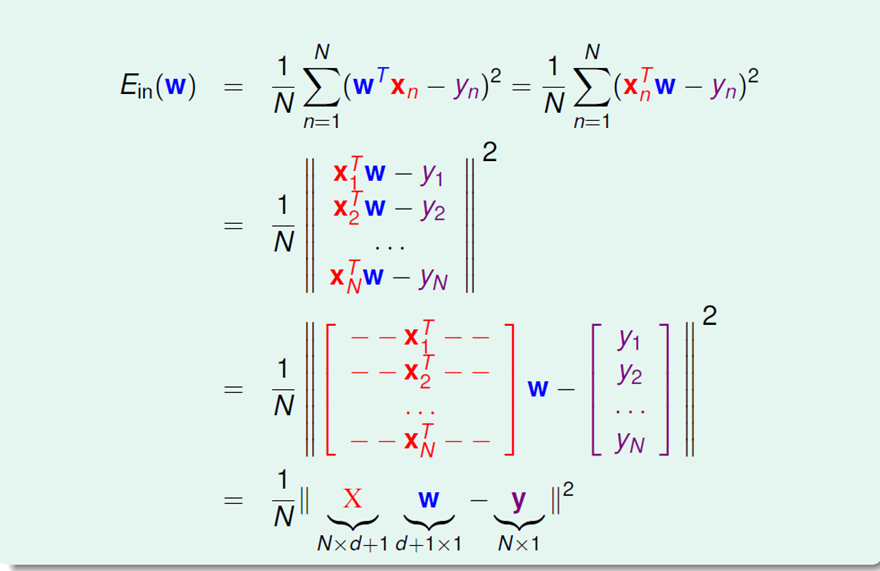
我们需要最小化E_in。

通过上式，可以看出E_in是continuous，differentiabl，convex函数，所以想让E_in最小，只需要让E_in的梯度（微分）等于0即可。

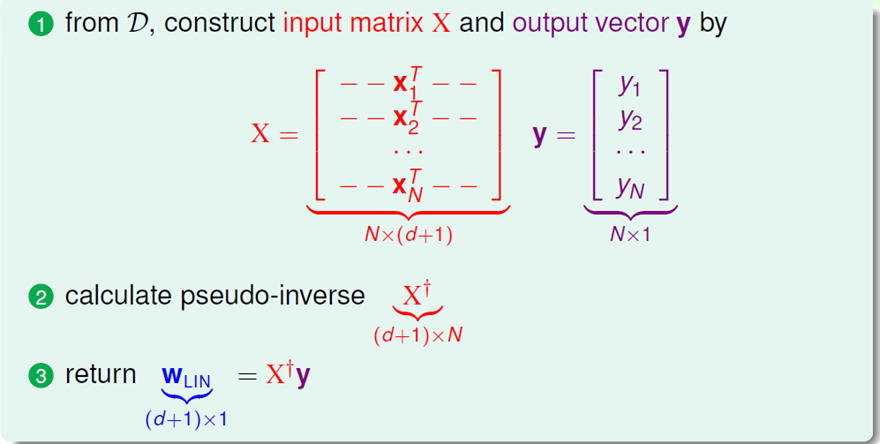
总结一下Linear Regression算法：

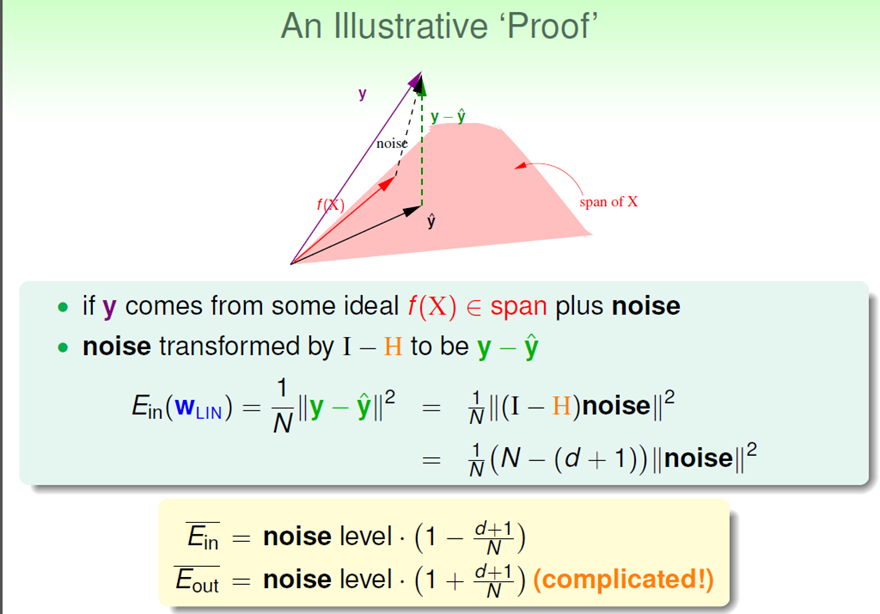
这里我们可以通过概率知识，求得E_in的大小：

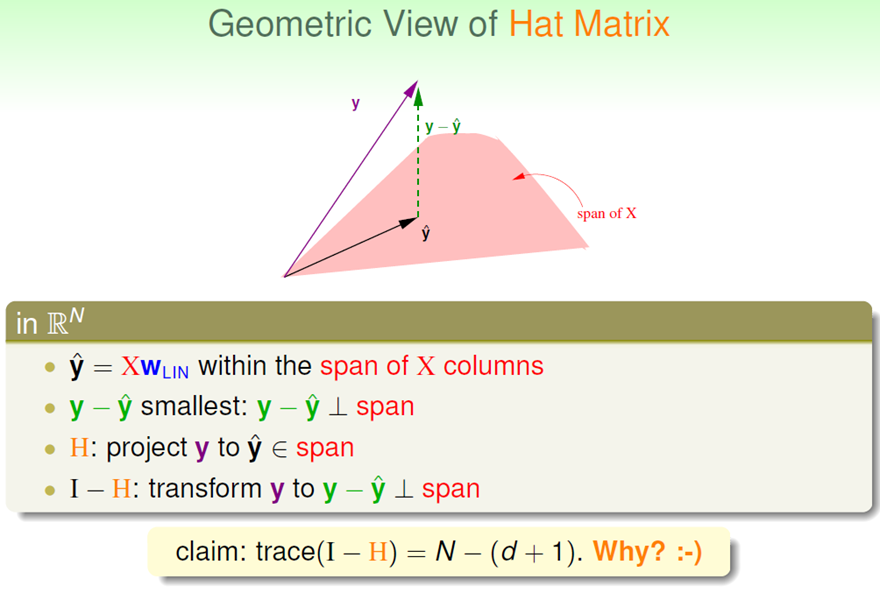
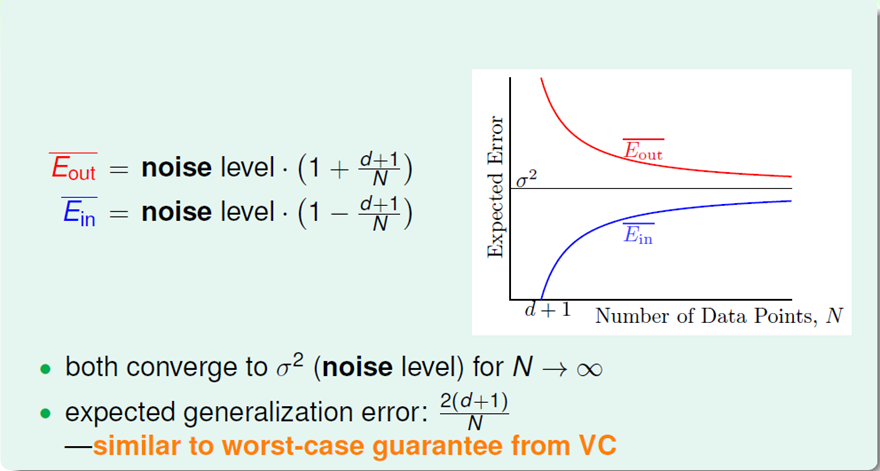
对于上面这一张PPT：所有的向量都在N维空间里，由（d+1）个N维x张成的span最多是d+1维的，H也是d+1维的，H将N维空间中的向量投影到span{X}中，而（I-H）将向量投影到与span{X}垂直的空间中，所以有trace（I-H）=N-(d+1)。（具体的可用数学证明）。

转载于:https://www.cnblogs.com/wangyanphp/p/5442988.html