四则运算---py实现

最新推荐文章于 2024-06-29 21:31:34 发布

转载最新推荐文章于 2024-06-29 21:31:34 发布 · 416 阅读

0 ·

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/NewBeeFly/p/8674754.html

文章标签：

#数据结构与算法

四则运算-二叉树

题目链接跳转：四则要求
源码已经上传至码云:四则运算

需求分析：

    1.实现带有自然数，真分数，假分数，少于3个运算符的四则等式
    2.实现查重，运算
    3.拥有万级别的出解题能力

功能设计：

    1.表达式中缀转后缀
    2.随机数字生成（包括真假分数）
    3.假分数转统一分数形式
    4.建树（顺便求解 按规则建树保证唯一）
    5.随便一种树的遍历方式
    6.表达式创建

程序设计

实现一个Tool工具类，一个节点类，一个等式类（实际上没什么卵用）

功能1：中缀转后缀

def nibolan(self,source):#参数为字符串表达式

功能2：操作数生成

def MyRandomData(self,begin=0):#随机操作数 默认从0随机

功能3：真假转化

def ToBeFraction(self,a):#转化为分数形式

功能4：建树并求解（查重关键点）

def createTree(self,source):#参数为后缀表达式字符串

功能5：遍历

def heng(self,a,b)：#a为root b为容器

功能6：表达式建立

def create(self):

代码说明：

查重思路

关键在于如何建立一颗 相同即唯一的树 按照上面当 ‘*+‘时才可能出现交换律等价的情况 所以采用上图的规则可解决这一问题。最后在创建
表达式的时候，遍历树并将节点记录下来，记录下来的字符串作为查重唯一码，若此码出现过则重新创建表达式（解释下为什么可以用遍历的
字符串来断定是否相同 虽然2种遍历才能唯一确定一颗树 相同遍历不一定相同字符串，但是如果表达式相同他必定有相同的遍历字符串 ，
也就是说他是一个子集的概念 大不了多做几次创建）

源码已经上传至码云:四则运算

运行测试：

开始

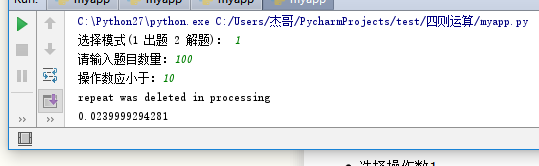
题目：

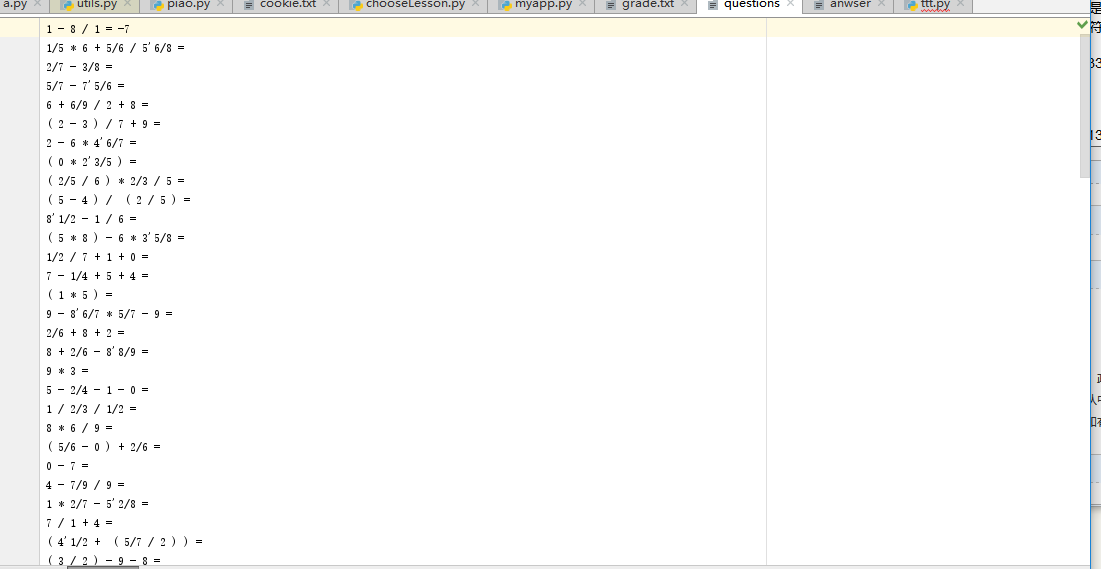
答案：

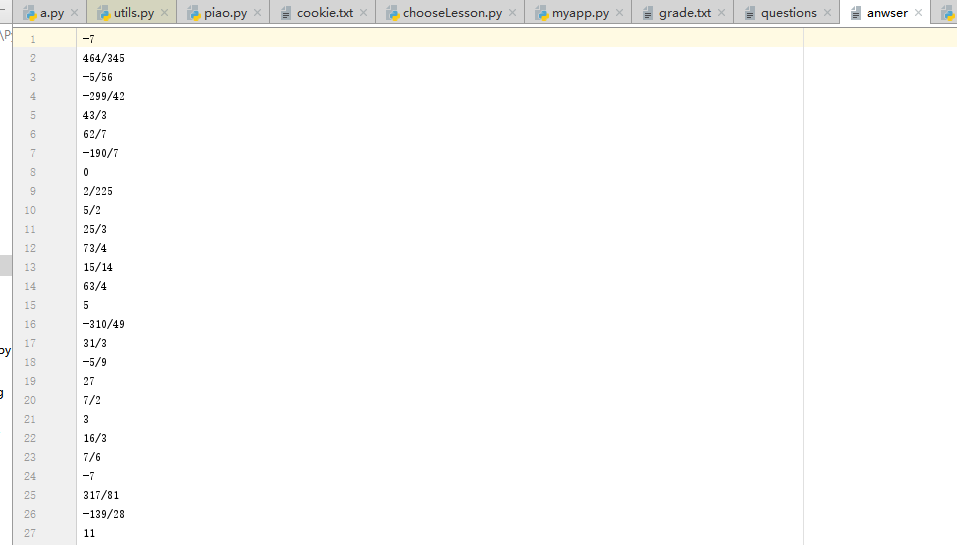
得分：

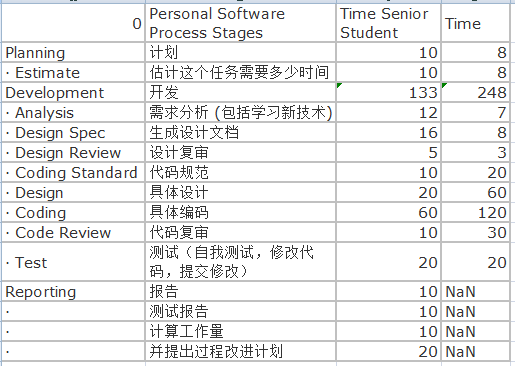
心得：

    多方式实现，多思考，多交流

转载于:https://www.cnblogs.com/NewBeeFly/p/8674754.html