[SWUST1740] 圆桌问题（最大流）

题目链接：https://www.oj.swust.edu.cn/problem/show/1740

看了讨论才发现不能多组输入，真坑。

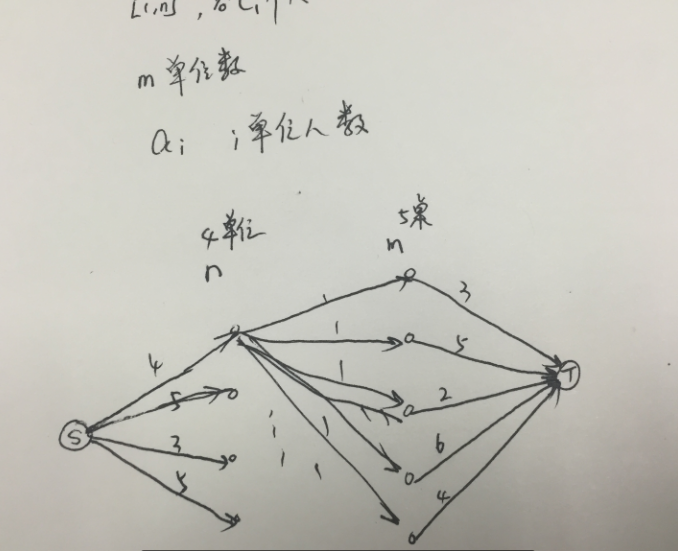
源点到n个单位，容量是每个单位的人数。

每个单位到每个桌子有1条边，容量为1。代表每个单位只能有一个人可以在那一张桌子。

桌子到汇点建边，容量为桌子最多坐的人数。

越来越熟练啦

 

  1 #include <bits/stdc++.h>
  2 using namespace std;
  3 
  4 typedef struct Edge {
  5     int u, v, w, next;
  6 }Edge;
  7 
  8 const int inf = 0x7f7f7f7f;
  9 const int maxn = 4444;
 10 
 11 int cnt, dhead[maxn];
 12 int cur[maxn], dd[maxn];
 13 Edge dedge[80001];
 14 int S, T, N;
 15 
 16 void init() {
 17     memset(dhead, -1, sizeof(dhead));
 18     for(int i = 0; i < maxn; i++) dedge[i].next = -1;
 19     S = 0; cnt = 0;
 20 }
 21 
 22 void adde(int u, int v, int w, int c1=0) {
 23     dedge[cnt].u = u; dedge[cnt].v = v; dedge[cnt].w = w; 
 24     dedge[cnt].next = dhead[u]; dhead[u] = cnt++;
 25     dedge[cnt].u = v; dedge[cnt].v = u; dedge[cnt].w = c1; 
 26     dedge[cnt].next = dhead[v]; dhead[v] = cnt++;
 27 }
 28 
 29 bool bfs(int s, int t, int n) {
 30     queue<int> q;
 31     for(int i = 0; i < n; i++) dd[i] = inf;
 32     dd[s] = 0;
 33     q.push(s);
 34     while(!q.empty()) {
 35         int u = q.front(); q.pop();
 36         for(int i = dhead[u]; ~i; i = dedge[i].next) {
 37             if(dd[dedge[i].v] > dd[u] + 1 && dedge[i].w > 0) {
 38                 dd[dedge[i].v] = dd[u] + 1;
 39                 if(dedge[i].v == t) return 1;
 40                 q.push(dedge[i].v);
 41             }
 42         }
 43     }
 44     return 0;
 45 }
 46 
 47 int dinic(int s, int t, int n) {
 48     int st[maxn], top;
 49     int u;
 50     int flow = 0;
 51     while(bfs(s, t, n)) {
 52         for(int i = 0; i < n; i++) cur[i] = dhead[i];
 53         u = s; top = 0;
 54         while(cur[s] != -1) {
 55             if(u == t) {
 56                 int tp = inf;
 57                 for(int i = top - 1; i >= 0; i--) {
 58                     tp = min(tp, dedge[st[i]].w);
 59                 }
 60                 flow += tp;
 61                 for(int i = top - 1; i >= 0; i--) {
 62                     dedge[st[i]].w -= tp;
 63                     dedge[st[i] ^ 1].w += tp;
 64                     if(dedge[st[i]].w == 0) top = i;
 65                 }
 66                 u = dedge[st[top]].u;
 67             }
 68             else if(cur[u] != -1 && dedge[cur[u]].w > 0 && dd[u] + 1 == dd[dedge[cur[u]].v]) {
 69                 st[top++] = cur[u];
 70                 u = dedge[cur[u]].v;
 71             }
 72             else {
 73                 while(u != s && cur[u] == -1) {
 74                     u = dedge[st[--top]].u;
 75                 }
 76                 cur[u] = dedge[cur[u]].next;
 77             }
 78         }
 79     }
 80     return flow;
 81 }
 82 
 83 const int maxm = 666;
 84 int n, m;
 85 int b[maxn], c[maxm];
 86 vector<int> path;
 87 
 88 int main() {
 89     // freopen("in", "r", stdin);
 90     scanf("%d%d",&n,&m);
 91     init();
 92     int sum = 0;
 93     for(int i = 1; i <= n; i++) {
 94         scanf("%d", &b[i]);
 95         sum += b[i];
 96     }
 97     for(int i = 1; i <= m; i++) scanf("%d", &c[i]);
 98     S = 0; T = n + m + 1; N = T + 1;
 99     for(int i = 1; i <= n; i++) adde(S, i, b[i]);
100     for(int i = 1; i <= m; i++) adde(i+n, T, c[i]);
101     for(int i = 1; i <= n; i++) {
102         for(int j = 1; j <= m; j++) {
103             adde(i, j+n, 1);
104         }
105     }
106     int ret = dinic(S, T, N);
107     if(ret != sum) {
108         puts("0");
109         return 0;
110     }
111     printf("1\n");
112     for(int i = 1; i <= n; i++) {
113         path.clear();
114         for(int j = dhead[i]; ~j; j=dedge[j].next) {
115             if(!dedge[j].w && dedge[j].v) path.push_back(dedge[j].v-n);
116         }
117         for(int j = path.size()-1; j >= 0; j--) printf("%d%c", path[j], j==0?'\n':' ');
118     }
119     return 0;
120 }

 

转载于:https://www.cnblogs.com/kirai/p/6798161.html