bzoj 3612: [Heoi2014]平衡【整数划分dp】-优快云博客

本文探讨了在-n~n范围内选取k个不同整数，使其和为0的组合计数问题。通过整数划分的概念，利用动态规划进行求解，避免重复和超限情况。文章提供了一个C++实现示例，详细展示了状态转移方程和边界条件的处理。

其实就是-n~n中求选k个不同的数，和为0的方案数
学到了新姿势叫整数划分，具体实现是dp 详见：https://blog.youkuaiyun.com/Vmurder/article/details/42551603
设f[i][j]为j个数和为i的方案数，然后因为互不相同，所以转移的话有两种，就是当前j个数全部+1，和当前j个数全部+1并且多填一个1出来，也就是f[i][j]=f[i-j][j]+f[i-j][j-1]
但是这里要求选的数不能超过n，我们考虑i>n的f中一定有一个大于n的数，我们把这种情况减掉就行了，也就是f[i][j]-=f[i-n-1][j-1]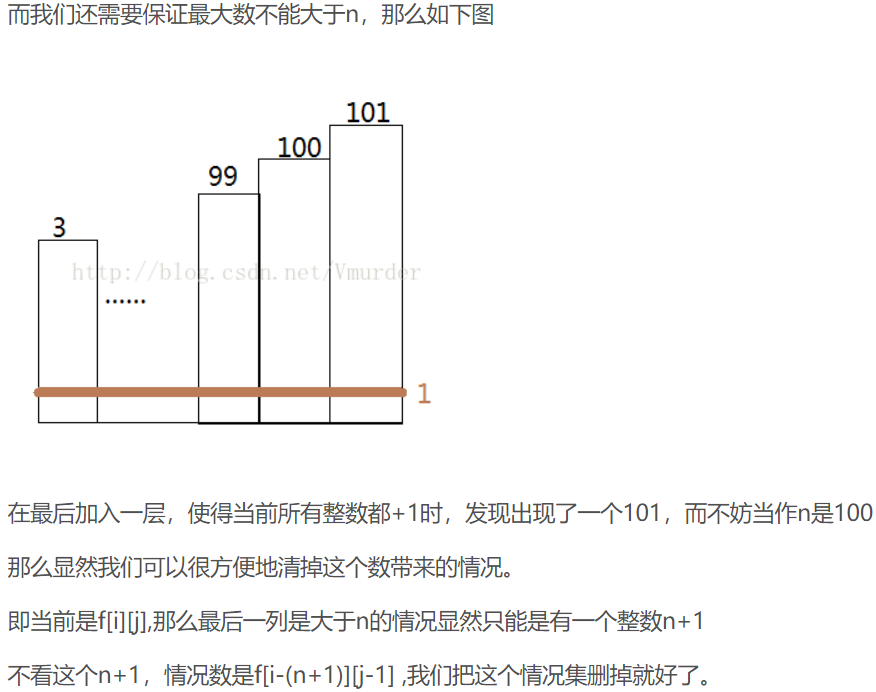

这是上面那个blog的截图

#include<iostream>
#include<cstdio>
using namespace std;
const int N=100005;
int T,n,m,mod,f[N][15],ans;
int read()
{
    int r=0,f=1;
    char p=getchar();
    while(p>'9'||p<'0')
    {
        if(p=='-')
            f=-1;
        p=getchar();
    }
    while(p>='0'&&p<='9')
    {
        r=r*10+p-48;
        p=getchar();
    }
    return r*f;
}
int main()
{
    T=read();
    while(T--)
    {
        n=read(),m=read(),mod=read();
        f[0][0]=1,ans=0;
        for(int i=1;i<=n*m;i++)
            for(int j=1;j<=m;j++)
            {
                if(i>=j)
                    f[i][j]=(f[i-j][j]+f[i-j][j-1])%mod;
                if(i>n)
                    f[i][j]=(f[i][j]-f[i-n-1][j-1]+mod)%mod;
            }
        for(int i=1;i<=n*m;i++)
            for(int j=1;j<=m;j++)
            {
                ans=(ans+f[i][j]*f[i][m-j])%mod;
                if(j!=m)
                    ans=(ans+f[i][j]*f[i][m-j-1])%mod;
            }
        printf("%d\n",ans+(m==1));
    }
    return 0;
}

转载于:https://www.cnblogs.com/lokiii/p/9641547.html