题目链接: http://acm.timus.ru/problem.aspx?space=1&num=1133
problem description: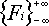
is an infinite sequence of integers that satisfies to Fibonacci condition
F
i + 2 =
F
i + 1 +
Fi for any integer
i. Write a program, which calculates the value of
Fn for the given values of
Fi and
Fj.
Input
The input contains five integers in the following order:
i,
Fi,
j,
Fj,
n.
−1000 ≤ i, j, n ≤ 1000, i ≠ j,
−2·10 9 ≤ Fk ≤ 2·10 9 ( k = min( i, j, n), …, max( i, j, n)).
−1000 ≤ i, j, n ≤ 1000, i ≠ j,
−2·10 9 ≤ Fk ≤ 2·10 9 ( k = min( i, j, n), …, max( i, j, n)).
Output
The output consists of a single integer, which is the value of
Fn.
Sample
| input | output |
|---|---|
3 5 -1 4 5 | 12 |
Hint
In the example you are given:
F
3 = 5,
F
−1 = 4; you asked to find the value of
F
5. The following Fibonacci sequence can be reconstructed using known values:
…,
F
−1 = 4,
F
0 = −1,
F
1 = 3,
F
2 = 2,
F
3 = 5,
F
4 = 7,
F
5 = 12, …
Thus, the answer is:
F
5 = 12.
解题分析:
对于fibonacci序列a,X0,X1,X2。。。。。b。假设这个序列是存在的。X是代表哪些未知的数。要如何才能判断这个序列是有解的呢?
给定a,b的值。枚举x0然后去确定b的那个空要填什么数,如果该数等于b那么就找到了解。然而貌似每次这样循环找速度会很慢的。fibonaccig公式
f[i] = f[i-1] + f[i-2] 线性方程,可以用矩阵来优化求第n项。
[f[1], f[0]] *[
11
01] = [f[2], f[1]], 令unit = [
11
0
1] , 求第n项,则先求矩阵ret = [f[1], f[0]] * unit^(n-1)


1 def matrixMul(a, b): 2 c = [[0 for i in xrange(2)] for j in xrange(2)] 3 for i in xrange(2): 4 for j in xrange(2): 5 for k in xrange(2): 6 c[i][j] += a[i][k]*b[k][j] 7 return c 8 9 def POW(unit, x): 10 a = unit; b = [ [1, 0], [0, 1] ] 11 while x>0: 12 if x&1: 13 b = matrixMul(b, a) 14 a = matrixMul(a, a) 15 x >>= 1 16 return b 17 18 def work(i, a, j, b, n): 19 unit = [ [1, 1], [1, 0] ] 20 mat = POW(unit, j-1) 21 l = -2000000000; r = 2000000000; mid = -1 22 while l<=r: 23 mid =(l+r)>>1 24 tmp = mid*mat[0][0]+a*mat[1][0] 25 if tmp > b: r = mid-1 26 elif tmp < b: l = mid+1 27 else : break 28 mat = POW(unit, n-1) 29 print mid*mat[0][0]+a*mat[1][0] if n>0 else a 30 31 if __name__ == '__main__': 32 i, a, j, b, n = map(int, raw_input().split()) 33 if i > j: 34 tmp = i; i = j; j = tmp 35 tmp = a; a = b; b = tmp; 36 j -= i; n -= i; i=0 37 work(i, a, j, b, n)























 406
406

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








