动态规划之0-1背包问题

最新推荐文章于 2020-11-29 17:43:43 发布

转载最新推荐文章于 2020-11-29 17:43:43 发布 · 150 阅读

0 ·

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/tsubasa/archive/2012/12/17/2821525.html

文章标签：

#数据结构与算法

本文详细介绍了两种背包问题的解决方法：0-1背包问题和无限背包问题。通过引入多阶段决策的最优化概念，利用动态规划算法实现问题求解，并提供了简化空间占用的滚动数组技巧。

1. 物品无限背包问题.

有n种物品, 每种都有无穷多个, 第i种物品体积为Vi, 重量为Wi. 选一些物品装到一个容量为C的背包里, 使得背包内物品总体积不超过C的前提下重量尽量大.1<n<=100,1<=Vi<=C<=10000,1<=Wi<=10^6

[分析] 带权的DAG最长路径问题, 把代码中的+1改为+W[i]即可.

2. 0-1背包问题

只凭"剩余体积"这个状态, 无法得知该物体是否被用过.

这里引入"多阶段决策的最优化": 用d(i,j)表示当前在第i层, 剩余容量为j时接下来的最大重量和.

则d(i,j)=max{d(i,j),d(i+1,j-V[i])+W[i]}, i>n时d(i,j) = 0, j<0时负无穷.

    for ( int i = n; i >= 1; i-- ) {
        for ( int j = 0; j < C; j++ ) {
            d[i][j] = ( i == n ) ? 0 : d[i+1][j];
            if ( j >= V[i] ) d[i][j] = MAX(d[i][j], d[i+1][j-V[i]] + W[i]);
        }
    }

运算过程示意:

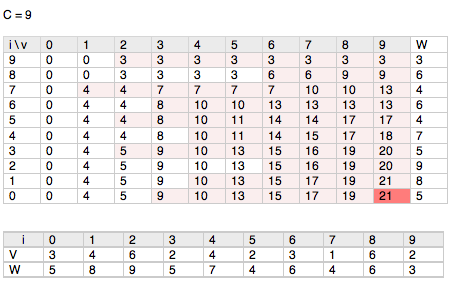
答案就在右下角d[0][C].

简化空间占用: 滚动数组

现在每次循环只用到2维表中的后两行数据, 而且第 i 行第 j 个数据只依赖第 i-1行中小于 j 的数据, 所以改一下内层循环的顺序就可以把二维数组简化成一维数组.

Tip:

在递推算法中, 如果计算顺序很特殊, 而且计算新状态所用到的原状态不多, 可以尝试使用滚动数组减少内存开销.

不过在使用滚动数组后, 解的打印变的困难了, 所以在需要打印方案甚至要求字典序的最小方案的场合, 应慎用滚动数组.

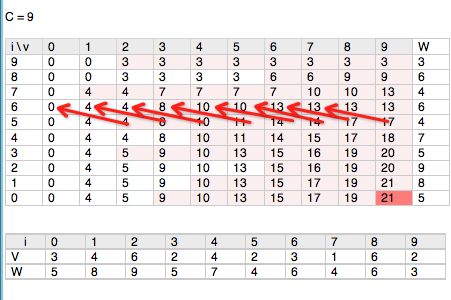
只要稍微改动一下代码~

for ( int i = n; i >=0; i-- ) {
        for ( int j = C; j >= 0; j-- ) {
            d[j] = ( i == n ) ? 0 : d[j];
            if ( j >= V[i] ) d[j] =  d[j] > d[j-V[i]] + W[i] ? d[j] : d[j-V[i]] + W[i];
            printf("%3d ", d[j]);
        }
        printf("\n");
}

转载于:https://www.cnblogs.com/tsubasa/archive/2012/12/17/2821525.html