在计算机视觉中,通过相机标定能够获取一定的参数,其原理是基于三大坐标系之间的转换和摄像机的畸变参数矩阵。在实验中经常用张正友标定发,进行摄像机标定,获取到内参数矩阵和外参数矩阵以及畸变参数矩阵。在应用中要区分三者作用。这也是在程序中函数输入量。
一、三大坐标系
在计算机视觉中,利用图像中目标的二维信息获取目标的三维信息,肯定需要相机模型的之间转化。
1、图像坐标系
在计算机系统中,描述图像的大小是像素,比如图像分辨率是1240*768.也就就是以为图像具矩阵rows是1024,cols是768.那图像的原点是在图像的左上角。
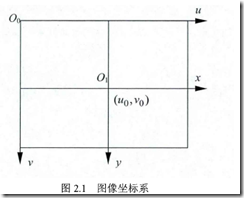
以图像左上角为原点建立以像素为单位的直接坐标系u-v。像素的横坐标u与纵坐标v分别是在其图像数组中所在的列数与所在行数。这是像素坐标,而不是物理坐标,为了后续的模型转换,有必要建立图像坐标系。
图像坐标系是以图像中心为原点,X轴和u轴平行,Y轴和v轴平行。dx和dy标示图像中每个像素在X轴和Y轴的物理尺寸,其实就是换算比例。比如图像大小是1024*768,图像坐标系x-y中大小为19*17.那么dx就是19/1024.
则图像中的每个像素在u-v坐标系中的坐标和在x-y坐标系中的坐标之间都存在如下的关系:

(上述公式中我们假设物理坐标系中的单位为毫米,那么dx的的单位为:毫米/像素。那么x/dx的单位就是像素了,即和u的单位一样都是像素)
为了使用方便,可将上式用齐次坐标与矩阵形式表示为:

其逆关系可表示为:

比如我们知道图像分辨率是1024*768,此时像素为(100,50),图像坐标系为是19*17mm。那么在图像坐标系是多少
根据转化和平移关系,知道U0为1024/2 = 512,v0位768/2 = 384.代入公式为x= (100-512)*19/1024.实际中图像坐标系还是比较容易获取。这是需要初始化,就能获取到的参数。
2、相机坐标系
a、相机坐标系概念
相机成像的几何关系可由图2.2表示。其中O点为摄像机光心(投影中心),Xc轴和Yc轴与成像平面坐标系的x轴和y轴平行,Zc轴为摄像机的光轴,和图像平面垂直。光轴与图像平面的交点为图像的主点O1,由点O与Xc,Yc,Zc轴组成的直角坐标系称为摄像机的坐标系。OO1为摄像机的焦距。

b、相机坐标系和图像坐标系之间的关系
在模型中我们将图像坐标放在相机坐标系前方,如图所示,两者之间的转化关系是有透镜原理获取的。

根据相似三角形的原理。X = (X/Z)*f。所以相机的焦距也是很重要的参数。y的获取同样道理。
实际中往往不会这么精确,会存在误差。
1、在实际中主点不一定在成像仪(图像平面)的中心,为了对光轴可能存在的偏移进行建模,我们引入两个新的参数:cx和cy。
2、在实际中,由于单个像素的在低价的成像仪上是矩形而不是正方形,我们引入了两个不同的焦距参数:fx和fy。(这里的焦距是以像素为单位)
则,我们假定物体在相机坐标系统中的点Q,其坐标为(X,Y,Z),以某些偏移的方式投影为点q(xsrceen,yscrreen),其中srceen为下表,坐标关系如下:
fx,fy和物理焦距F之间的关系为:fx=Fsx和fy=Fsy。其中sx表示x方向上的1毫米长度所代表像素值,即单位像素/每毫秒,fx,fy是在相机标定中整体计算的,而不是通过该公式计算的。
3、世界坐标系
世界坐标系是为了描述相机的位置而被引入的,如图2.2中坐标系OwXwYwZw即为世界坐标系。平移向量t和旋转矩阵R可以用来表示相机坐标系与世界坐标系的关系。所以,假设空间点P在世界坐标系下的齐次坐标是(Xw,Yw,Zw,1)T,(这里T是上标转置),在相机坐标下的齐次坐标是(Xc,Yc,Zc,1)T,则存在如下的关系:

上式中R是3×3的正交单位矩阵(也成为旋转矩阵),t是三维的平移向量。矢量0=(0,0,0),M1是4×4矩阵。
在实验中,比如我们设定经纬坐标是(48,42,15)的为世界坐标系的原点,X方向指向正北。但是在试验场中点(46,40,5)是相机坐标的系的原点,方向是正东。那么两者之间就存在一个转换关系。
1、旋转矩阵R:
通常,任何维的旋转可以表示为坐标向量与合适尺寸的方阵的乘积。最终一个旋转等价于在另一个不同坐标系下对点位置的重新表述。坐标系旋转角度θ,则等同于目标点绕坐标原点反方向旋转同样的角度θ。图11-8显示了矩阵乘法对二维旋转的描述。在三维空间中,旋转可以分解为绕各自坐标轴的二维旋转(例如图11-8就是绕z轴旋转),其中旋转的轴线的度量保存不变(这就是为什么旋转矩阵为正交矩阵的缘由)。如果依次绕x,y,z轴旋转角度ψ,φ和θ,那么总的旋转矩阵R是三个矩阵Rx(ψ),Ry(φ),Rz(θ)的乘积,其中:


因此R=Rx(ψ),Ry(φ),Rz(θ).在绕X轴旋转时,到YZ的平面距离没有变化,所以X坐标没有变化,只是YZ坐标需要诚意旋转系数,其他矩阵同理。这个需要记住即可
平移向量T:
平移向量用来表示怎么样将一个坐标系的原点移动到另外一个坐标系的原点,或者说平移向量是第一个坐标系原点与第二个坐标系原点的偏移量。因此,从以目标中心为原点的坐标系移动到以摄像机为中心的原点的另外一个坐标系,相应的平移向量为T=目标原点—摄像机原点。那么点在世界坐标系的中的坐标Po到在摄像机坐标系中Pc:
Pc=R(Po-T)
故,用三个角度ψ,φ和θ表示三维旋转,用三个参数(x,y,z)表示三维平移,共6个参数,对摄像机而言,OpenCV内参数矩阵有4个参数:fx,fy,cx,cy。故对于每一个视场的解需要10个参数。我们知道一个四边形的4个点可以提供8个方程,故至少需要两个视角才能解出全部几何参数。8*2=6+6+4。
二、相机模型
在计算机视觉中通过相机模型讲三维空间的点和二维图像中的点联系起来。如果不考虑畸变的原因,则是线性模型,如果考虑,则是非线性模型。
1、线性模型
可用针孔模型来近似表示任一点P(Xc,Yc,Zc)在像平面的投影位置,也就是说,任一点P(Xc,Yc,Zc)的投影点p(x,y)都是OP(即光心(投影中心)与点P(Xc,Yc,Zc)的连线)与像平面的交点如上一篇文章中的图2.2。对应比例关系可得:

(说明:Xc的c下表表示camera相机,上述公式是在相机坐标系内,利用三角形相似原理,即x/f=Xc/Z,其中上述公式的单位为毫米,f表示焦距单位毫米)
上式可以用齐次坐标与矩阵的形式表示为:

将上一篇文章中的(2.3)和(2.4)代入(2.6)式就可以得到点P的世界坐标与其投影坐标(u,v)之间的关系为:

(说明:上述公式中完成了从世界坐标系到图像坐标系的转变,中间经过了相机坐标系的过度,Xw中的w表示world世界,单位为毫米,而u,v是的 单位为像素,即完成了从毫米——像素的转换。)
其中ax=f/dx,ay=f/dy;M是3×4的矩阵—投影矩阵,M1完全由相机的内参数ax,ay,u0,v0决定,(u0,v0)为主点坐标,ax,ay分别表示图像u轴和v轴上的尺度因子,M2则完全由相机的外部参数决定。而相机标定就是确定相机的内外参数。
由式(2.7)可知,若已知相机的内外参数,则相当于已知投影矩阵M.当已知M和空间点P的坐标:矢量Xw=(Xw,Yw,Zw,1)T,(矢量Xw上面有一个矢量标识杠,T表示矢量的转置)。式(2.7)可以给出三个方程,消去Zc就可以得到其投影点p的坐标(u,v)(其实也就是我用一个相机就可以拍摄一个物体的图片了)。但是由于M为3×4不可逆矩阵,当 点P的投影坐标(u,v)和投影矩阵M为已知时,我们只能得到关于Xw,Yw,Zw的两个线性方程,即射线OP的方程,由上一篇图2.2我们可以看出,位于射线OP上的所有空间点的投影点(即图像点)都是p点。所以不能唯一确定空间点P的世界坐标矢量Xw.
2、非线性模型
1、径向畸变
现实中第一是由于成像平面和透镜平面不死绝对平行的,所以存在径向畸变。对径向畸变成像仪中心是畸变为0,越到边缘畸变越严重,比如鱼眼透镜。
对于便宜的网络摄像机,我们通常使用前两项,其中通常第一项为k1,而第二项为k2。对畸变很大的摄像机,比如鱼眼透镜,我们使用第三个径向畸变项k3。通常成像仪某点的径向位置按下式调节:

这里(x,y)是畸变点在成像仪上的原始位置,(xcorrected,ycorrected)表示矫正后的新位置。
2、切向畸变
切向畸变是由于透镜制造上的缺陷使得透镜本身与图像平面不平行而产生的。径向畸变可以有两个额外的参数p1和p2来描述,如下:

因此总共有5个我们需要的畸变参数。由于在OpenCV程序中5个参数是必需的,所以它们被放置到一个畸变向量中,这是一个5×1的矩阵,按顺序依次包含k1,k2,p1,p2和k3。

在实际的成像过程中,考虑镜头的失真,一般都存在非线性畸变,所以线性模型不能准确描述成像几何关系。非线性畸可用下列公式描述:



若考虑非线性畸变,则对相机标定时需要使用非线性优化算法。而有研究表明引入过多的非线性参入(如离心畸变和薄棱畸变)不仅不能提高精度,还会引起解的不稳定。一般情况下径向畸变就足以描述非线性畸变,所有本课题只是考虑径向畸变。则将式(2.9)中的径向畸变代入式(2.8)可得:

单个摄像头的定标主要是计算出摄像头的内参(焦距f和成像原点cx,cy、 五个畸变参数(一般只需要计算出k1,k2,p1,p2,
对于鱼眼镜头等径向畸变特别大的才需要计算k3))以及外参 (标定物的世界坐标)。
所以,为了得到空间物体的三维世界坐标,就必须有两个或更多的相机构成立体视觉系统模型才能实现。
三 、单目标定矩阵关系
根据前面两章节的介绍,描述了坐标系之间的转化,同时也讲解了畸变矩阵的由来。那如果获取到图像中二维坐标,如何获取到现实中三维坐标呢?当然单目摄像机无法获取三维坐标,但能反映一定关系。综上来讲,矩阵变换公式为:


根据坐标系之间转化和相机模型(线性和非线性模型),研究了极几何及基本矩阵的知识,证明了基本矩阵是求得摄像机投影矩阵的关键,根据基本矩阵F和摄像机标定阶段获取的内参数矩阵K,计算得到本质矩阵E,通过对E进行奇异值分解求得外参数矩阵R,T,接着求出投影矩阵P1和P2.




 本文详细介绍了计算机视觉中的相机标定原理,包括三大坐标系(图像坐标系、相机坐标系、世界坐标系)之间的转换关系,以及相机模型中的线性与非线性模型。此外还探讨了如何通过标定获取相机的内外参数。
本文详细介绍了计算机视觉中的相机标定原理,包括三大坐标系(图像坐标系、相机坐标系、世界坐标系)之间的转换关系,以及相机模型中的线性与非线性模型。此外还探讨了如何通过标定获取相机的内外参数。

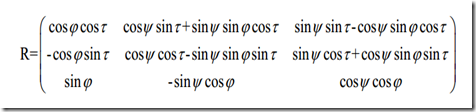
















 794
794

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








