HDU 6060 RXD and dividing（思维+计算贡献值）

http://acm.hdu.edu.cn/showproblem.php?pid=6060

题意：

给定一棵 n 个节点的树，1 为根。现要将节点 2 ~ n 划分为 k 块，使得每一块与根节点形成的最小斯坦纳树的边权值总和最大。

 

思路：

这道题目应该往边的贡献值方向去思考，对于u（非1）结点，设它与它父亲结点的边为e，它的子节点分的块越多，那么e这条边的贡献值也就越大，因为每一分块都需要e这条边来连通。所以我们就要尽量让每条边的贡献值都最大。

 

下面图解一下：（分成 3 part的情况）

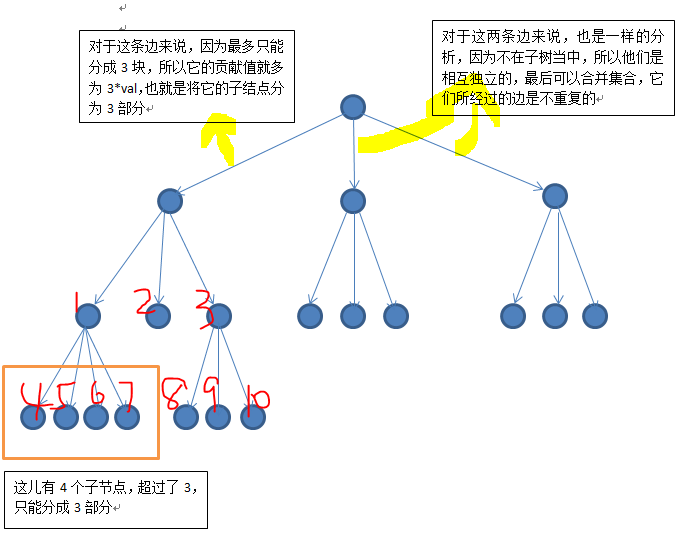
4、5、6、7由于超过了3，所以只能分成3部分，我们可以假设性的分为{4,5}，{6}，{7}这样3组，1和3是没有子树关系的，所以可以把它们合并进去，不会影响3结点边的贡献值，

现在又可以假设性的分为{4,5,8}，{6,9}，{7,10}这样三组，将2结点合并进去后可以变成{4,5,8}，{2,6,9}，{7,10}这样三组，此时1、2、3、4、5、6、7、8、9这几个结点的边都已经达到了它们所能达到的最大贡献值。

依次向上分析即可。

所以，我们可以得出结论，每条边的最大贡献值就是min（sz[u]，k），最后将所有边的贡献值加起来即可。

 1 #include<iostream>
 2 #include<algorithm>
 3 #include<cstring>
 4 #include<cstdio>
 5 #include<sstream>
 6 #include<vector>
 7 #include<stack>
 8 #include<queue>
 9 #include<cmath>
10 #include<map>
11 #include<set>
12 using namespace std;
13 typedef long long ll;
14 typedef pair<int,int> pll;
15 const int INF = 0x3f3f3f3f;
16 const int maxn = 1000000 + 5;
17 
18 int n, k;
19 
20 int sz[maxn];
21 int val[maxn];
22 vector<pll> G[maxn];
23 
24 void dfs(int u, int fa)
25 {
26     sz[u]=1;
27     for(int i=0;i<G[u].size();i++)
28     {
29         int v=G[u][i].first;
30         if(v==fa)  continue;
31         val[v]=G[u][i].second;
32         dfs(v,u);
33         sz[u]+=sz[v];
34     }
35 }
36 
37 int main()
38 {
39     //freopen("in.txt","r",stdin);
40     while(~scanf("%d%d",&n,&k))
41     {
42         for(int i=1;i<=n;i++)  G[i].clear();
43 
44         for(int i=1;i<n;i++)
45         {
46             int u,v,w;
47             scanf("%d%d%d",&u,&v,&w);
48             G[u].push_back(make_pair(v,w));
49             G[v].push_back(make_pair(u,w));
50         }
51 
52         dfs(1,-1);
53         ll ans=0;
54         for(int i=1;i<=n;i++)
55             ans+=(ll)val[i]*min(k,sz[i]);
56         printf("%lld\n",ans);
57     }
58     return 0;
59 }

转载于:https://www.cnblogs.com/zyb993963526/p/7272125.html