基于随机变量一系列最基本的概念,我们便会开始探讨一些随机变量函数的期望、多个随机变量和的期望、多个随机变量乘积的期望。
这里我们就简单的讨论后两个期望。
这两个问题可以基于如下的一个现实模型:
同时掷n个骰子(或者说掷骰子n次),n个筛子的得到点数的和的期望是多少?n个筛子得到点数的乘积的期望是多少?
为了解决这个问题,我们观察如下的两个式子:
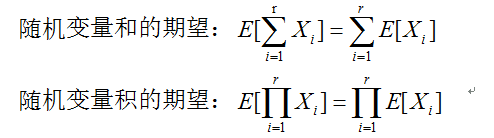
如果这两个式子成立,那么我们对一个有重复试验的过程,只需基于被重复的那个单位的相关参数便计算整个试验的参数。例如在上面的模型当中,如果等式成立,我们就可以基于掷骰子1次得到的结果,来计算掷n个筛子得到的结果。
那么上式是否正确呢?我们结合期望的概念推导一下便知道了。


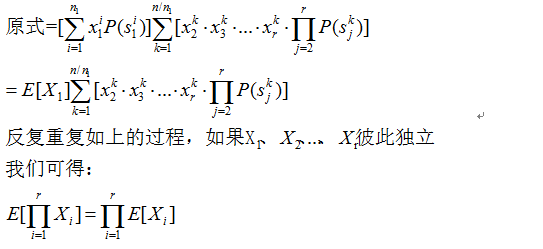







 本文通过掷骰子的实例,探讨了多个随机变量和的期望与乘积的期望的计算方法,并介绍了如何利用单个随机变量的特性推导出整体期望的公式。
本文通过掷骰子的实例,探讨了多个随机变量和的期望与乘积的期望的计算方法,并介绍了如何利用单个随机变量的特性推导出整体期望的公式。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








