逆序对统计与分治法-优快云博客

题目要求:
在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数P。并将P对1000000007取模的结果输出。即输出P%1000000007

输入描述:题目保证输入的数组中没有的相同的数字

数据范围：

对于%50的数据,size<=10^4

对于%75的数据,size<=10^5

对于%100的数据,size<=2*10^5

示例1 输入 1,2,3,4,5,6,7,0 输出 7

第一反应是顺序扫描整个数组。每扫描到一个数组的时候，逐个比较该数字和它后面的数字的大小。

如果后面的数字比它小，则这两个数字就组成了一个逆序对。假设数组中含有n个数字。由于每个数字都要和O(n)这个数字比较，因此这个算法的时间复杂度为O(n^2)。

更好的方法是分治法,是对归并进行改进,复杂度为 nlog(n),在此之前可以回顾下归并排序

https://www.cnblogs.com/chengxiao/p/6194356.html

https://www.cnblogs.com/skywang12345/p/3602369.html

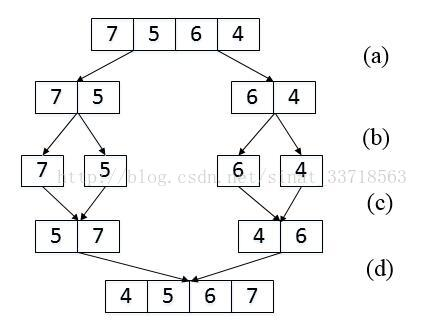
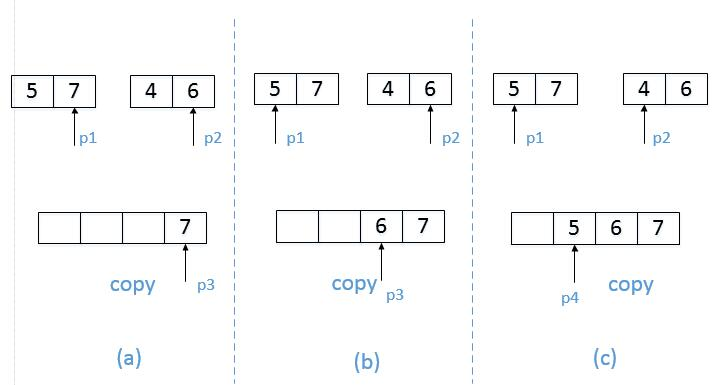
我们以数组{7,5,6,4}为例来分析统计逆序对的过程。每次扫描到一个数字的时候，我们不拿ta和后面的每一个数字作比较，否则时间复杂度就是O(n^2)，因此我们可以考虑先比较两个相邻的数字

(a) 把长度为4的数组分解成两个长度为2的子数组；

(b) 把长度为2的数组分解成两个成都为1的子数组；

(d) 把长度为2的子数组合并、排序，并统计逆序对；

在上图（a）和（b）中，我们先把数组分解成两个长度为2的子数组，再把这两个子数组分别拆成两个长度为1的子数组。接下来一边合并相邻的子数组，一边统计逆序对的数目。在第一对长度为1的子数组{7}、{5}中7大于5，因此（7,5）组成一个逆序对。同样在第二对长度为1的子数组{6}、{4}中也有逆序对（6,4）。由于我们已经统计了这两对子数组内部的逆序对，因此需要把这两对子数组排序如上图（c）所示，以免在以后的统计过程中再重复统计。

接下来我们统计两个长度为2的子数组子数组之间的逆序对。合并子数组并统计逆序对的过程如下图所示。

我们先用两个指针分别指向两个子数组的末尾，并每次比较两个指针指向的数字。如果第一个子数组中的数字大于第二个数组中的数字，则构成逆序对，并且逆序对的数目等于第二个子数组中剩余数字的个数，如下图（a）和（c）所示。如果第一个数组的数字小于或等于第二个数组中的数字，则不构成逆序对，如图b所示。每一次比较的时候，我们都把较大的数字从后面往前复制到一个辅助数组中，确保辅助数组（记为temp）中的数字是递增排序的。在把较大的数字复制到辅助数组之后，把对应的指针向前移动一位，接下来进行下一轮比较。

 1 public class Solution {
 2     //将逆序数的对数设置为全局变量
 3     int cnt=0;
 4     public int InversePairs(int [] array) {
 5         if(array != null){
 6              RecusionSorted(array,0,array.length - 1);
 7         }
 8         return  cnt%1000000007;
 9     }
10     public void RecusionSorted(int data[] , int start , int end ) {
11         if(start < end) {
12             //不停地递归拆分,然后再一步步的合并merge
13             int mid = (start + end) >> 1;
14             RecusionSorted(data,start,mid);
15             RecusionSorted(data,mid+1,end);
16             MegerArray(data,start,mid,end);
17         }
18     }
19     //合并规则
20     public void MegerArray(int[] data, int start, int mid, int end) {
21         int temp[] = new int[end-start+1]; 
22         //在2个子数组中统计逆序数的对数
23         //左指针i 指向 左字数组的最后一位mid
24         //右指针j 指向 右字数组的最后一位end
25         //指针m 指向 右字数组的起始位
26         int i  =  mid;
27         int j = end;
28         int m = mid+1;
29         int z = 0;//遍历或者赋值temp数组
30         while(j >= m && i >= start) {
31             //左子数组的i值 大于 右子数组的j值 
32             //那么左边i的这个数 一定大于包括j在内的之前的所有数(因为默认有序了)
33             if(data[i] > data[j]) {
34                 temp[z++] = data[i--];//把大的拿出来,放进temp数组中,在temp中形成有序数组
35                 cnt += (j-mid)%1000000007;
36                 //测试用例输出结果比较大，对每次返回的count mod(1000000007)求余
37                 cnt %= 1000000007;
38             }else {
39                 //左子数组的i值 小于等于 右子数组的j值,不构成逆序数
40                 //j减减,i不动,j大,将j放进有序数组temp中
41                 temp[z++] = data[j--];
42             }
43         }
44         //左子数组遍历完了,剩下右子数组了,将剩下的放进temp中构成有序数组
45         while(j >= m) {
46             temp[z++] = data[j--];
47         }
48         //右子数组遍历完了,剩下左子数组了,将剩下的放进temp中构成有序数组
49         while(i >= start) {
50             temp[z++] = data[i--];
51         }
52         //start和end从始至终就没有被赋值改变过
53         //将temp从尾到前赋值给原来的数组data,在后面的判断中不会导致顺序出错
54         for(int k = start ; k <= end ; k ++) {
55             data[k] = temp[end - k];
56         }
57     }
58 }