返回一个整数数组中最大子数组的和

一：题目内容及设计思路

1.题目：

　　返回一个整数数组中最大数组的和

2.要求：

　　（1）输入一个整数数组，数组里有正数也有负数。

　　（2）数组中连续的一个或多个整数组成一个子数组，每个子数组都有一个和。

　　（3）求所有子数组的和的最大值。有球时间复杂度为O(n)。

3.设计思路：

　　（1）利用while循环输入各个整数，用getchar()函数判断while循环是否结束，当用户按下回车键时，即getchar()=='\n'时，跳出while循环；

　　（2）记录下循环的次数，即数组长度；

　　（3）调用函数Compare(int Group[],int Length)对输入的数组进行判断比较，返回最大子数组的和；

　　（4）在Compare函数中用递归思路进行最大子数组和的判断。

4.结对开发伙伴：

　　姓名：程思敏

　　博客名：鹏程万里之思

　　博客地址链接：http://home.cnblogs.com/u/pengchengwanli/

二：具体实现

1.实验代码：

//返回一个整数数组中最大子数组的和
#include<iostream>
#define N 100
using namespace std;

int Compare(int Group[], int Length)
{
	int MaxSum[N][2];
	//MaxSum[N][0]表示前N-1个数中，最大的子数组和
	//MaxSum[N][1]表示前N-1个数的最大的子数组和加第N个数的和与第N个数相比的最大值
	MaxSum[0][0] = MaxSum[0][1] = Group[0];
	for (int i = 1; i < Length; i++)
	{
		MaxSum[i][0] = __max(MaxSum[i - 1][0], MaxSum[i - 1][1]);
		MaxSum[i][1] = __max(MaxSum[i - 1][1] + Group[i], Group[i]);
	}
	return __max(MaxSum[Length - 1][0], MaxSum[Length - 1][1]);
}

int main()
{
	int Number[N];	//整数数组
	int length;	//数组长度
	cout << "请输入一个整型数组：" << endl;
	cin >> Number[0];
	length = 1;
	while (getchar() != '\n')
	{
		cin >> Number[length++];
	}
	cout << "该数组中的最大的子数组和为：";
	cout << Compare(Number, length) << endl;
	return 0;
}

2.运行结果截图

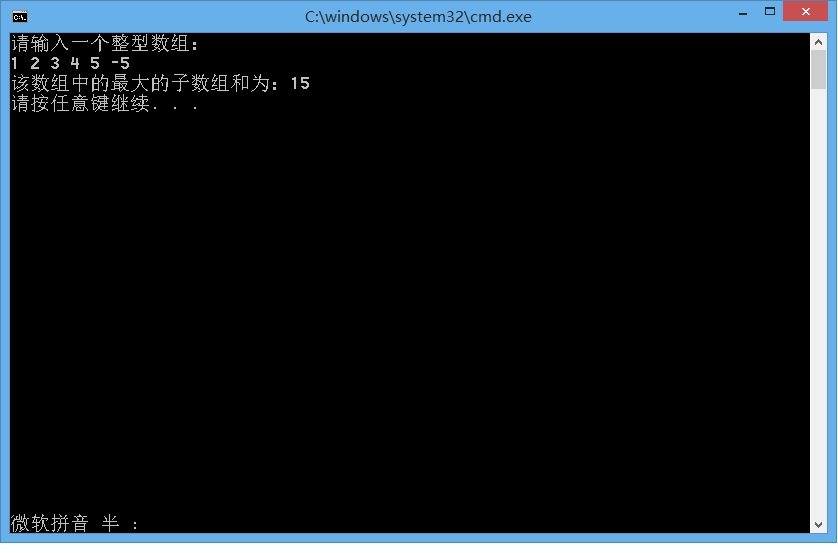
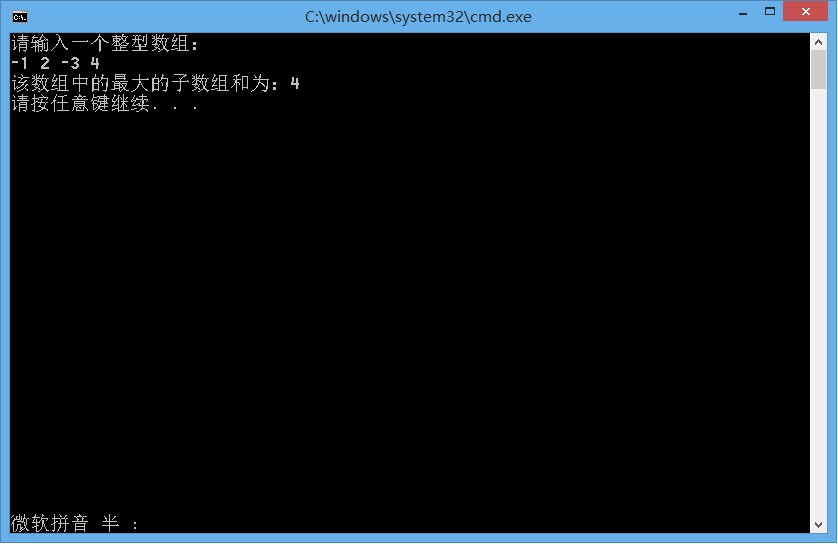
三：总结

本次实验要说难也不难，主要是算法不清楚，后来经过查阅相关的书籍，还是解决了问题。

项目计划总结：

日期\任务	听课	编写程序	查阅资料	日总计
星期一	2		1	3
星期二
星期三			1	1
星期四	2			2
星期五		1		1
星期六		2		2
星期日
周总计	4	3	2	9

 

时间记录日志：

日期	开始时间	结束时间	中断时间	静时间	活动	备注
3/21	14：00	15：50	10	100	听课	软件工程
	19:  30	20:  40	10	60	查阅资料	查阅数据结构课本
3/22
3/23	19：20	20：20		60	查阅资料	查阅数据结构课本
	14：20	15：30	10	60	编写程序	编写周二的程序
3/24	14：00	15：50	10	100	听课	软件工程
3/25	19：30	20：40	10	60	编写程序	编写周二的程序
3/26	9：20	11：40	10	130	编写程序	编写周四的程序
	13：20	14：20		60	写博客	写博客
3/27

缺陷记录日志：

日期	编号	引入阶段	排除阶段	修复时间&问题描述
3/21	1
3/22	2
3/23	3	编码	查询资料	编写程序，没弄明白getchar()函数，半小时后解决问题
3/24	4
3/25	5	编码	调试	编写程序，调试，解决递归问题，程序完成
3/26	6
3/27	7

转载于:https://www.cnblogs.com/wangzongze/p/5322901.html