Back propagation(BP)

*图片来源:图片来源为: http://galaxy.agh.edu.pl/~vlsi/AI/backp_t_en/backprop.html

一.BP算法的直观理解

一个多层感知器(Multilayer perceptron)可以表示为下图.

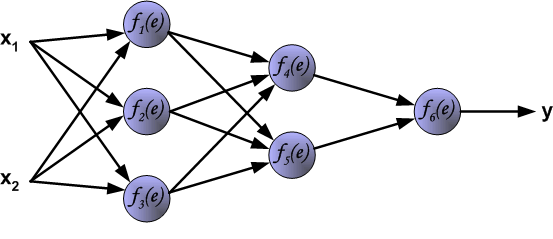
s中 x$_1$, x$_2$为输入, y为输出, e = w$_i1$x$_1$ + w$_i2$x$_2$. 左式方程组成的感知器可以很好地表达一个线性函数, 但无法表达非线性函数.现实生活中我们遇到的问题多为非线性的, 因此需要引入激活函数f. 常见的激活函数有 tanh, sigmoid, ReLu等. 不同的激活函数可以将输出映射到不同的值. 具体可见另一篇关于激活函数博文(可能还没写).

在BP算法被发明以前, 训练多层感知器是很困难的. 因为多层感知器隐藏层(图中f$_4$和f$_5$)的输出是未知的, 所以无法像单层感知器那样学习. BP算法可以由以下图片直观理解.

 

 　　1. feedforward

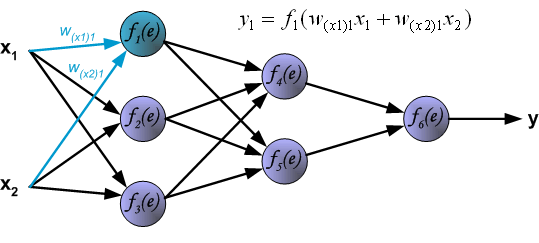
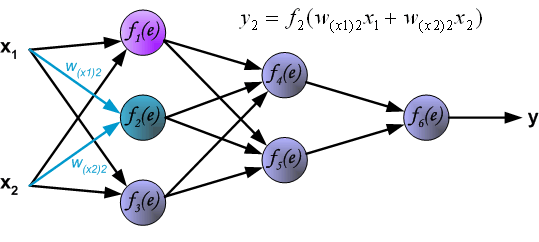
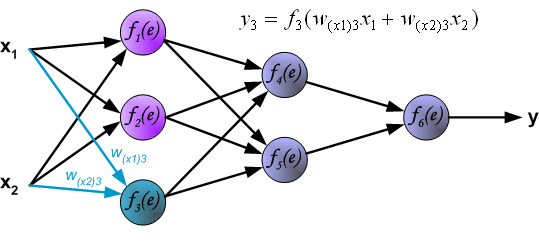
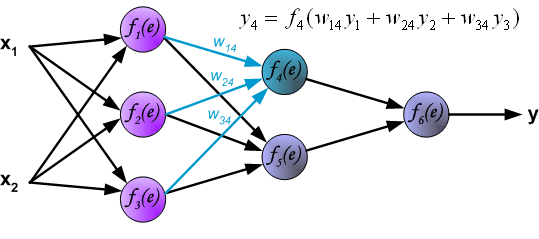
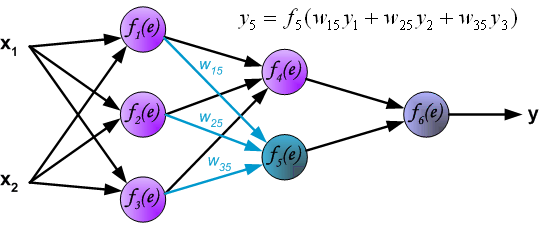
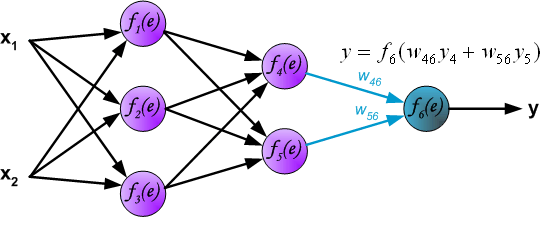
　　2. back propagation

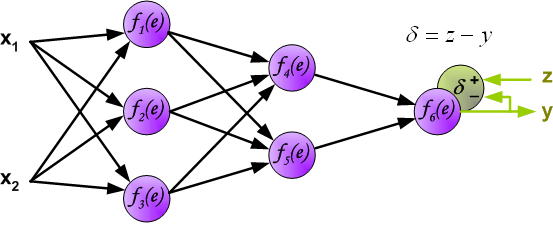
　　在分类问题中, 假设有c个标签, N个待分类样本, 则误差计算为: E$^N$ = $\frac{1}{2}(\sum_{n=1}^N\sum_{k=1}^c(t^n_k-y^n_k)^2)$, 其中, $t^n_k$为第k个样本对标签n的目标输出值, $y^n_k$为该样本k对n标签网络输出值, 则$(t^n_k-y^n_k)^2$表示第k个样本对于第n个标签的误差. 只有当样本属于某个标签时, $t^n$为正,其余为零或负.

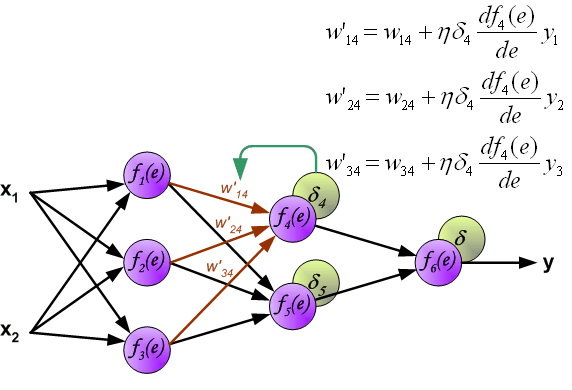
　　如上所述, 隐含层的目标输出是未知的, 因此我们只能通过链式法则将误差后向传播至中间的隐含层:

 

 

 

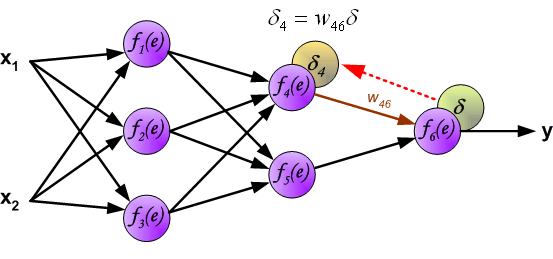
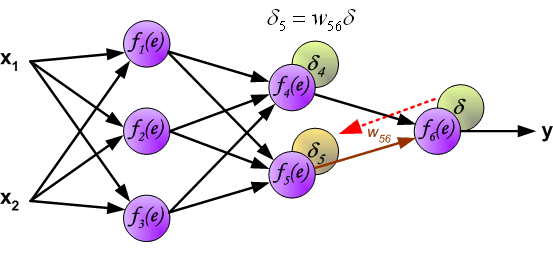
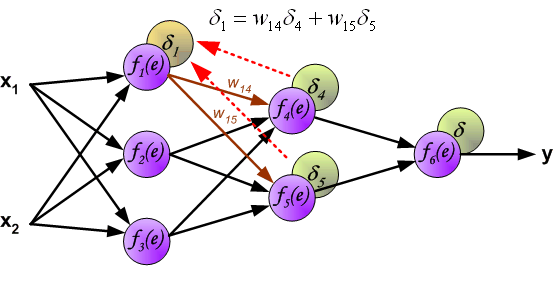
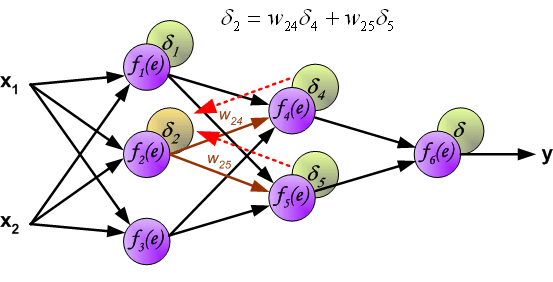
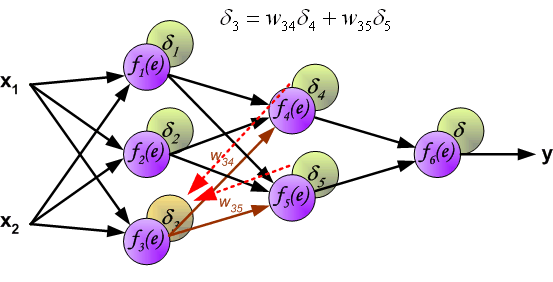
权值更新如下, 其中η为学习率, 更新公式的推导见第二节梯度下降:

 

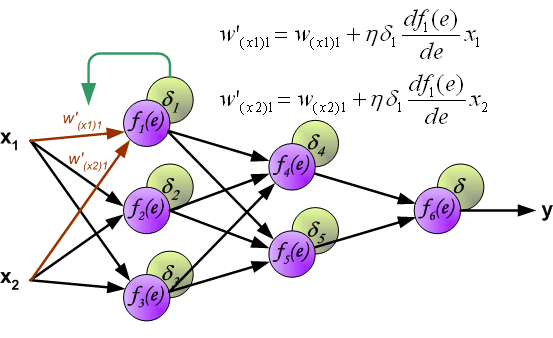
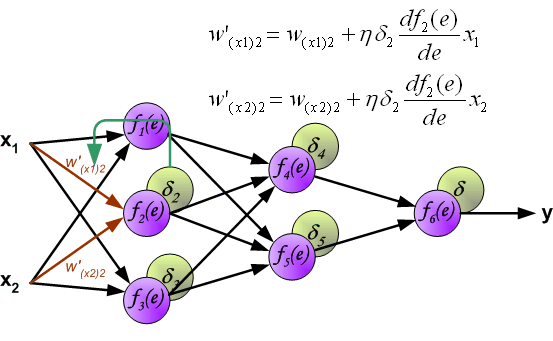
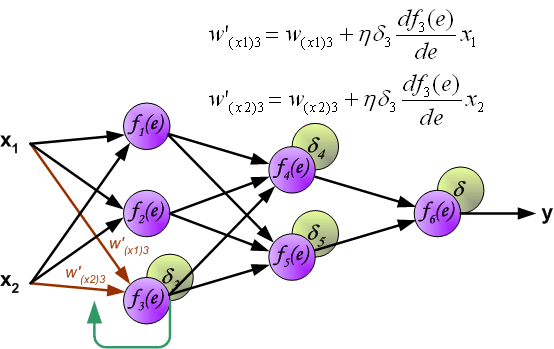
二. 梯度下降(Gradient Descent)

梯度下降是神经网络以及深度学习中最常用的学习算法. 有监督学习中, 我们在学习时通过一个cost function来描述网络输出与正确label的误差, 并通过cost function对权值w和偏置求偏导, 使它们根据如下公式更新:

其中 J(W,b)为cost function, α为学习率. 经过多次迭代更新, W和b将更新至J(W,b)处于极小值(*并非最小值).

MLP中, 我们也通过梯度下降法进行学习. 但如上一节所说, 隐含层的"正确输出"是未知的(这也是它被称为隐含层的原因), 我们无法对每一层定义相应的cost function. 在BP算法发明以前, 人们固定输出层以外的隐含层的权值并只更新最后一层的权值. 此时最后一层就决定了学习的好坏. 

BP算法引入了残差的概念.

 

　　1.我们首先进行前向传导, 得到L$_2$, L$_3$...L$_l$的节点的输出值. 第L$_l$层第i个节点输出为.

 

　　2.输出后, 我们将输出层L$_n$的残差定义为网络产生的激活值和实际值的差距 :

 

　　3.通过对第L$_l+1$层的残差加权平均计算第L$_l$层节点i的残差, 该残差表示该节点对输出残差的影响. 这样, 输出残差就反向传播至前面所有层数:

 

 　　　　   左式我们需要对所有层数的激活函数进行求导. 在激活函数为sigmoid时, 我们可以证明: 

 

 

　　4. 根据各层残差, 我们可以计算出J(W,b)对W和b的偏导, 实现更新:

 

　　　　

 

 

reference:

　　UFLDL 

转载于:https://www.cnblogs.com/xyzt0000/p/6103032.html