公茂果老师的课件中,给出了四种多项式求值的算法,下面给出代码示例:
课件地址:http://see.xidian.edu.cn/faculty/mggong/chn.htm
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%E-mail: jtailong@163.com
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
num=[10 50 100 150 200 300 400 500 10000 20000 50000 100000];
x=input('please enter x:') %求解相应x的多项式的值
for m=1:1:12 %从1至12,步长为1
a=rand(1,num(m)+1); %生成相应的序列a
%方法一:直接代入法
tic; %开始计时
p1(m)=polyval(a,x);
t1(m)=toc;
%方法二:递归法一
tic;
p2(m)=0;
for j=1:1:(num(m)+1)
p2(m)=p2(m)+a(j)*x^(j-1);
end
t2(m)=toc;
%方法三:递归法二
tic;
p3(m)=0;
q=1;
for j=1:1:(num(m)+1)
q=q*x;
p3(m)=p3(m)+a(j)*q;
end
t3(m)=toc;
%方法四:递归法四
tic;
p4(m)=0;
for j=1:num(m)
p4(m)=x*p4(m)+a(num(m)+2-j); %百度文库中出现的算法,会漏掉一个点值
end
t4(m)=toc;
end
%画图
g=semilogx(num,t1,'r+',num,t2,'b*',num,t3,'g:',num,t4,'k-.');
legend('一','二','三','四');
set(g,'linestyle',':','linewidth',2.0,'markersize',8);
xlabel('num=10 ,50 ,100 ,150 ,200, 300 ,400, 500 ,10000, 20000, 50000 ,100000');
ylabel('time');
title('温酒待君归四线比较图')
grid on;
下面是结果的显示:
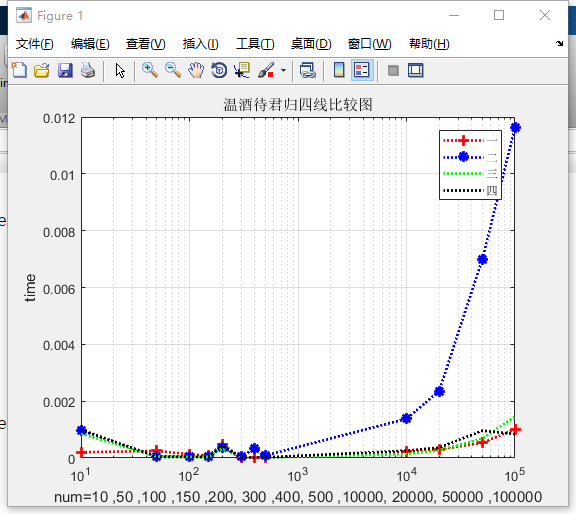
参考链接 https://wenku.baidu.com/view/c3f6f2b8c5da50e2534d7f42.html







 本文介绍了公茂果老师课件中的四种多项式求值算法,并通过MATLAB代码实现对比了这些方法的时间效率。直接代入法、两种递归法及另一种特殊递归法被应用于不同规模的数据集上,实验结果显示了各种算法的性能差异。
本文介绍了公茂果老师课件中的四种多项式求值算法,并通过MATLAB代码实现对比了这些方法的时间效率。直接代入法、两种递归法及另一种特殊递归法被应用于不同规模的数据集上,实验结果显示了各种算法的性能差异。
















 1809
1809

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








