牛顿法可以用于求解方程,优化问题。牛顿法在最优化问题中每步都要求Hessian矩阵,计算比较复杂,拟牛顿法通过正定矩阵近似Hessian矩阵,简化了这一计算过程。
#@author: gr
#@date: 2014-01-30
#@email: forgerui@gmail.com一、 Talyor公式
\(f(x)\)具有直到\((n+1)\)阶的导数,有
\[ f(x) = f(x_0) + f'(x_0)(x - x_0) + \dfrac{f''(x_0)}{2!}(x - x_0)^2 + \cdots + \dfrac{f^n(x_0)}{n!}(x - x_0)^n + R_n(x)\]
其中,
\[R_n(x) = \dfrac{f^{(n+1)(\xi)}}{(n+1)!}(x - x_0)^{n+1}\]
二、Jacobian & Hessian
1. Jacobian矩阵
假设\(F: R_n \rightarrow R_m\) 是一个从欧式n维空间转换到欧式m维空间的函数。这个函数由m个实函数组成:\(y_1(x_1,\cdots , x_n), \cdots , y_m(x_1, \cdots , x_n)\)。则Jacobian矩阵如下:
$$ J = \begin{bmatrix} \dfrac{\partial y_1}{\partial x_1} & \dfrac{\partial y_1}{\partial x_2} & \cdots & \dfrac{\partial y_1}{\partial x_n} \\ \dfrac{\partial y_2}{\partial x_1} & \dfrac{\partial y_2}{\partial x_2} & \cdots & \dfrac{\partial y_2}{\partial x_n}\\ \vdots & \vdots & \ddots & \vdots & \\ \dfrac{\partial y_n}{\partial x_1} & \dfrac{\partial y_n}{\partial x_2} & \cdots & \dfrac{\partial y_n}{\partial x_n} \end{bmatrix} $$
如果$ m = n\(时,那么F就变成了\)n \times n$ 维的函数,它的雅可比矩阵是一个方阵。
2. Hessian矩阵
海森矩阵(Hessian matrix或Hessian)是一个自变量为向量的实值函数的二阶偏导数组成的方块矩阵,函数如下:
\[ f(x_1, x_2, \cdots , x_n)\]
如果\(f\)的所有二阶导数都存在,那么\(f\)的海森矩阵即:
\[ H(f)_{ij} (x) = D_i D_j f(x) \]
其中\(x = (x_1, x_2, \cdots , x_n)\),即\(H(f)\)为:
$$ \left[ \begin{matrix} \dfrac{\partial^2f}{\partial x_1^2} & \dfrac{\partial^2f}{\partial x_1 \partial x_2 } & \cdots & \dfrac{\partial^2f}{\partial x_1 \partial x_n }\\ \dfrac{\partial^2f}{\partial x_2 \partial x_1} & \dfrac{\partial^2f}{\partial x_2^2} & \cdots & \dfrac{\partial^2f}{\partial x_2 \partial x_n }\\ \vdots & \vdots & \ddots & \vdots \\ \dfrac{\partial^2f}{\partial x_n \partial x_1} & \dfrac{\partial^2f}{\partial x_n \partial x_2} & \cdots & \dfrac{\partial^2f}{\partial x_n^2 }\\ \end{matrix} \right] $$
海森矩阵可以被应用于牛顿法解决的大规模优化问题.
三、 求解方程 (Newton's Method)
有方程\(f(x) = 0\),当求解这个方程很困难时可以使用牛顿法。
根据Talyor公式,有
\[f(x) \approx f(x_k) + (x - x_k) ~ f'(x_k)\]
令\(f(x) = 0\),有
\[f(x_k) + (x - x_k) ~ f'(x_k) = 0\]
设这个方程的解为\(x_{k+1}\),那么有
\[ x_{k+1} = x_k - \dfrac{f'(x_k)}{f(x_k)}\]
这里,\(f(x_{k+1})\) 比 \(f(x_k)\) 更接近0,这样通过不停地迭代,可以在 \(f(x^*) = 0\) 时收敛。整个过程如下图:

求解方程\(f(x) = \cos(x)\cdot x^3\),从 \(x_0 = 0.5\) 开始迭代,过程如下:
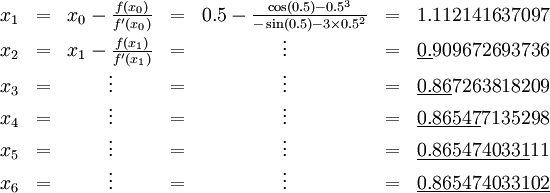
四、 优化问题 (Newton's Method)
很多优化问题都需要使用梯度下降法或牛顿法去求解。
根据Taylor公式,
\[f(x) = f(x_k + \Delta x) = f(x_k) + f'(x_k) \Delta x + \dfrac{1}{2}f''(x) \Delta x^2\]
当\(\Delta x\)趋近于0时,两边约去\(f(x_k +\Delta x)\)和\(f(x_k)\), 有
\[f'(x_k) \Delta x + \dfrac{1}{2}f''(x) \Delta x^2 = 0\]
对\(\Delta x\)求导,进一步求解 \(x\) 有
\[ x_{k+1} = x_k - \dfrac{f'(x)}{f''(x)}\]
上面讨论的是2维的情况,如何考虑高维的情况。
考虑无约束最优化问题
\[min_{x \in R^n} f(x)\]
假设在\(x^*\)处取到极小点。
将 \(f(x)\) 在 \(x_k\) 处进行二阶泰勒展开:
\[f(x) = f(x_k) + g_k^T(x - x_k) + \dfrac{1}{2}(x - x_k)^T H(x_k)(x - x_k) \]
其中,\(g_k = g(x_k) = \nabla f(x_k)\) 是 \(f(x)\) 的梯度向量在点 \(x_k\) 的值,\(H(x_k)\) 是 \(f(x)\) 的Hessian矩阵。
\[H(x) = \left[ \begin{array}{c} \dfrac{\partial^2f}{\partial x_i \partial x_j} \end{array} \right]_{n \times n}\]
有
\[x_{k+1} = x_k - H_k^{-1}g_k\]
五、 拟牛顿法
上面的方法求\(H_k^{-1}\)比较复杂,考虑用一个n阶矩阵\(G_k\)来近似替代它。
\[g_{k+1} - g_k = H_k(x_{k+1} - x_k)\]
记 \(y_k = g_{k+1} - g_k\),\(\delta_k = x_{k+1} - x_k\),则,
\[ y_k = H_k \delta_k\]
如果\(H_k\)是正定的,保证牛顿法搜索方向是下降方向。
\[x_{k+1} = x_k - \lambda H_k^{-1} g_k\]
\(f(x)\) 在泰勒展开式可以近似写成:
\[f(x) = f(x_k) - \lambda g_k^TH_k^{-1}g_k\]
因为\(H_k^{-1}\)是正定的,故有 \(g_k^T H_k^{-1} g_k > 0\)。当\(\lambda\)为一个充分小的正数时,总有\(f(x) < f(x_k)\),也就是说是下降方向。
拟牛顿法,将\(G_k\)作为\(H_k^{-1}\)的近似,要求矩阵\(G_k\)满足同样的条件。首先,\(G_k\)是正定的。同时,满足下面的拟牛顿条件:
\[G_{k+1} y_k = \delta_k\]
按照拟牛顿条件,在每次迭代中可以选择更新矩阵\(G_{k+1}\):
\[G_{k+1} = G_k + \Delta G_k \]







 本文介绍了牛顿法及其在优化问题中的应用,包括求解方程和解决大规模优化问题的方法。同时,文章阐述了拟牛顿法的原理,以及如何通过正定矩阵近似Hessian矩阵来简化计算过程。本文详细解释了Talyor公式、Jacobian矩阵、Hessian矩阵的概念,并提供了求解方程和优化问题的具体步骤。
本文介绍了牛顿法及其在优化问题中的应用,包括求解方程和解决大规模优化问题的方法。同时,文章阐述了拟牛顿法的原理,以及如何通过正定矩阵近似Hessian矩阵来简化计算过程。本文详细解释了Talyor公式、Jacobian矩阵、Hessian矩阵的概念,并提供了求解方程和优化问题的具体步骤。
















 2815
2815

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








