P3358 最长k可重区间集问题-优快云博客

本文探讨了在给定的开区间集合中寻找最长k可重叠区间集的问题，采用MCMF（最小费用最大流）算法解决。通过离散化处理区间端点，构建网络流模型，实现对复杂区间覆盖问题的有效求解。

\(\color{#0066ff}{题目描述}\)

对于给定的开区间集合 I 和正整数 k，计算开区间集合 I 的最长 k可重区间集的长度。

\(\color{#0066ff}{输入格式}\)

第 1 行有 2 个正整数 n和 k，分别表示开区间的个数和开区间的可重迭数。接下来的 n行，每行有 2 个整数，表示开区间的左右端点坐标。

\(\color{#0066ff}{输出格式}\)

将计算出的最长 k可重区间集的长度输出

\(\color{#0066ff}{输入样例}\)

\(\color{#0066ff}{输出样例}\)

\(\color{#0066ff}{数据范围与提示}\)

对于100%的数据，\(1\le n\le 500,1\le k\le 3\)

\(\color{#0066ff}{题解}\)

区间端点离散化

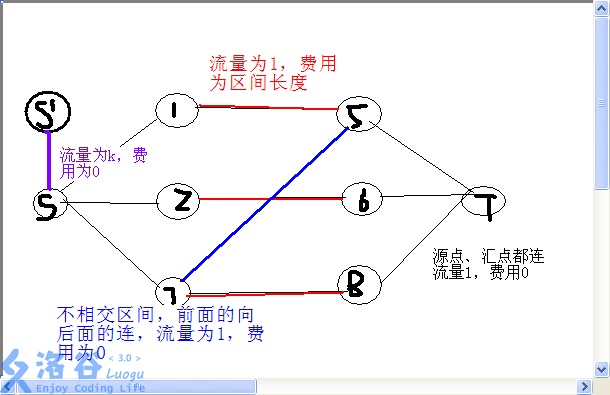
起点根1连，权为k（保证不超过k），终点根末端连

每个点直接连容量inf

区间左右端点连容量为1（只用一次），权为len的边

引用xuxinyu的blog的图

#include <bits/stdc++.h>
#define _ 0
#define LL long long
inline LL in() {
    LL x = 0, f = 1; char ch;
    while(!isdigit(ch = getchar()))(ch == '-') && (f = -f);
    while(isdigit(ch)) x = x * 10 + (ch ^ 48), ch = getchar();
    return x * f;
}

struct node {
    int to, dis, can;
    node *nxt, *pre;
    node(int to = 0, int dis = 0, int can = 0, node *nxt = NULL)
        :to(to), dis(dis), can(can), nxt(nxt) {}
    void *operator new (size_t) {
        static node *S = NULL, *T = NULL;
        return (S == T) && (T = (S = new node[1024]) + 1024), S++;
    }
};
std::queue<int> q;
typedef node* nod;
int n, k, s, t, cnt;
const int maxn = 5050;
const int inf = 0x7fffffff;
int dis[maxn], change[maxn], l[maxn], r[maxn], B[maxn];
nod head[maxn], road[maxn];
bool vis[maxn];
void add(int from, int to, int can, int dis) {
    nod o = new node(to, dis, can, head[from]);
    head[from] = o;
}

void link(int from, int to, int can, int dis) {
    add(from, to, can, dis);
    add(to, from, 0, -dis);
    head[from]->pre = head[to];
    head[to]->pre = head[from];
}

bool spfa() {
    for(int i = s; i <= t; i++) dis[i] = -inf, change[i] = inf;
    dis[s] = 0;
    q.push(s);
    while(!q.empty()) {
        int tp = q.front(); q.pop();
        vis[tp] = false;
        for(nod i = head[tp]; i; i = i->nxt)
            if(dis[i->to] < dis[tp] + i->dis && i->can) {
                dis[i->to] = dis[tp] + i->dis;
                road[i->to] = i;
                change[i->to] = std::min(change[tp], i->can);
                if(!vis[i->to]) vis[i->to] = true, q.push(i->to);
            }
    }
    return change[t] != inf;
}

void mcmf() {
    int cost = 0;
    while(spfa()) {
        cost += dis[t] * change[t];
        for(int i = t; i != s; i = road[i]->pre->to) {
            road[i]->can -= change[t];
            road[i]->pre->can += change[t];
        }
    }
    printf("%d", cost);
}

int main() {
    n = in(), k = in();
    for(int i = 1; i <= n; i++) {
        l[i] = in(), r[i] = in();
        B[++cnt] = l[i], B[++cnt] = r[i];
    }
    std::sort(B + 1, B + cnt + 1);
    int len = 1;
    for(int i = 2; i <= cnt; i++) 
        if(B[i] != B[i - 1]) 
            B[++len] = B[i];
    cnt = len;
    for(int i = 1; i <= n; i++) {
        l[i] = std::lower_bound(B + 1, B + cnt + 1, l[i]) - B;
        r[i] = std::lower_bound(B + 1, B + cnt + 1, r[i]) - B;
    }
    s = 0, t = cnt + 1;
    link(s, 1, k, 0);
    link(cnt, t, inf, 0);
    for(int i = 1; i < cnt; i++) link(i, i + 1, inf, 0);
    for(int i = 1; i <= n; i++) link(l[i], r[i], 1, B[r[i]] - B[l[i]]);
    mcmf();
    return 0;
}

转载于:https://www.cnblogs.com/olinr/p/10184004.html