[SPOJ2021] Moving Pebbles

最新推荐文章于 2019-03-18 14:46:20 发布

转载最新推荐文章于 2019-03-18 14:46:20 发布 · 132 阅读

0 ·

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/LMSH7/p/9573410.html

本文解析了[SPOJ2021]MovingPebbles问题，探讨了两人游戏策略，根据石堆数量及分布判断胜负，并提供了C++实现代码。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

[SPOJ2021] Moving Pebbles

题目大意:给你\(N\)堆\(Stone\)，两个人玩游戏. 每次任选一堆，首先拿掉至少一个石头,然后移动任意个石子到任意堆中. 谁不能移动了，谁就输了

Solution

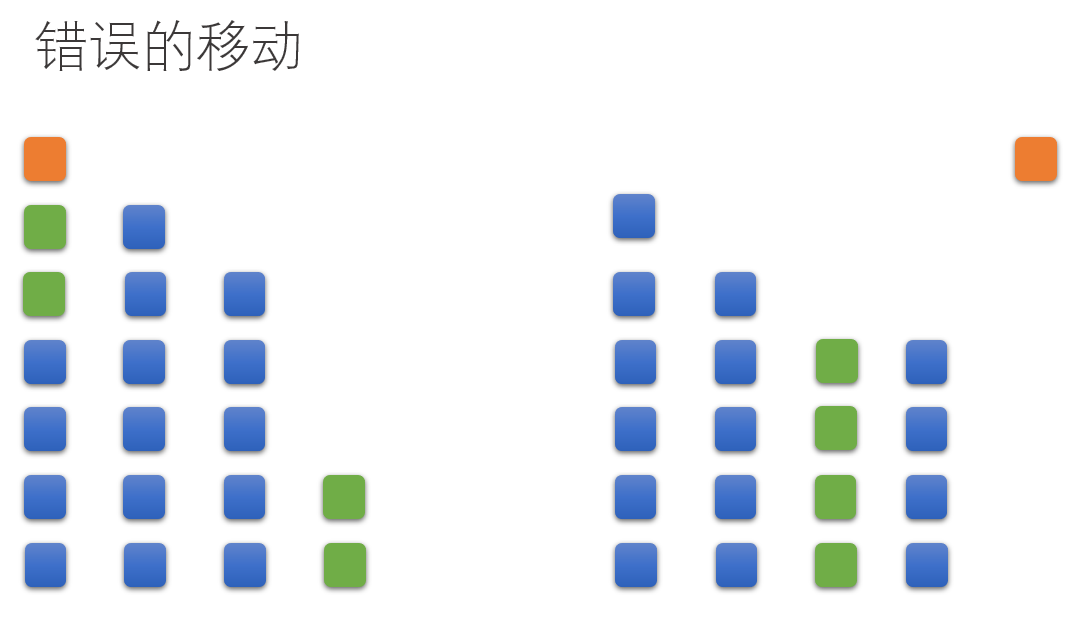
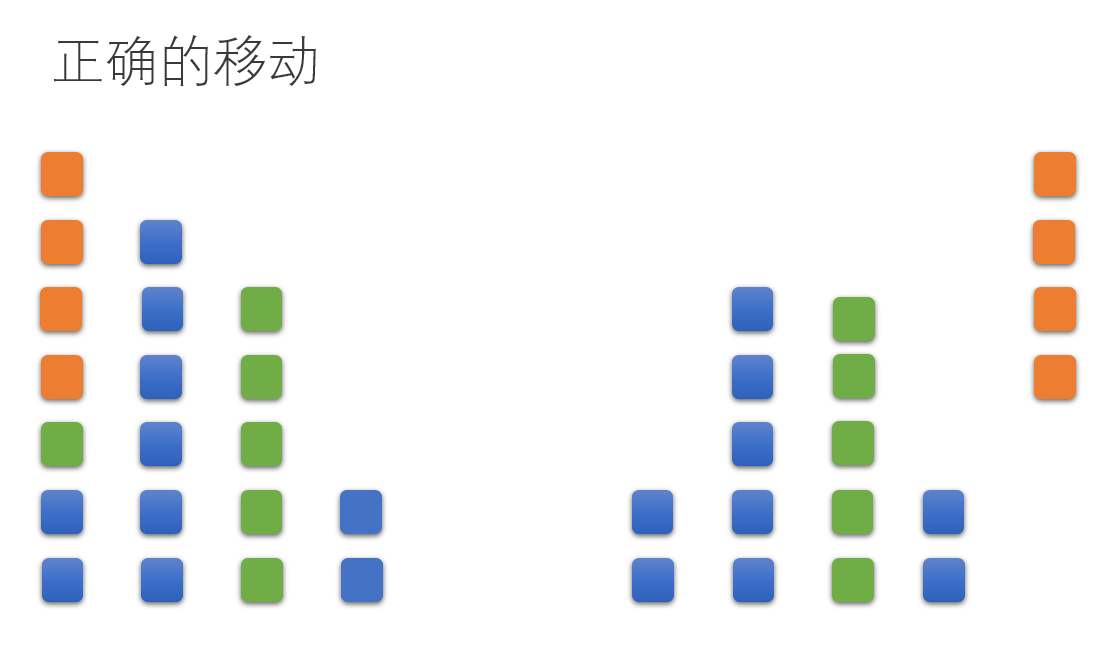
n为偶数，这些石子堆都是可以两两配对的石子堆,后手必胜，那么无论如何先手对它移动,后手都可以对另一个配对的石子堆做相应的调整.
n为偶数，但是石子不可以两两配对,先手必胜，可以令最高堆与最低堆相同，然后将其他堆的石子数补成两两相同。
\(n\)为奇数，先手必胜，因为先手一定可以操作最高的一堆使得局面变成偶数堆且两两堆数相同。

Code

#include <cstdio>
#include <algorithm>

int a[100005];

int read() {
    int x = 0; char c = getchar();
    while (c < '0' || c > '9') c = getchar();
    while (c >= '0' && c <= '9') {
        x = (x << 3) + (x << 1) + (c ^ 48);
        c = getchar();
    }
    return x;
}

int main() {
    int n = read();
    for (int i = 1; i <= n; ++i) a[i] = read();
    std::sort(a + 1, a + n + 1);
    for (int i = 1; i <= n; i += 2)
        if(a[i] != a[i+1]){
            puts("first player");
            return 0;
        }
    puts("second player");
    return 0;
}

转载于:https://www.cnblogs.com/LMSH7/p/9573410.html