UVA1533-Moving Pegs（BFS+状态压缩）

Problem UVA1533-Moving Pegs

Accept：106  Submit：375

Time Limit: 3000 mSec

 Problem Description

 

 

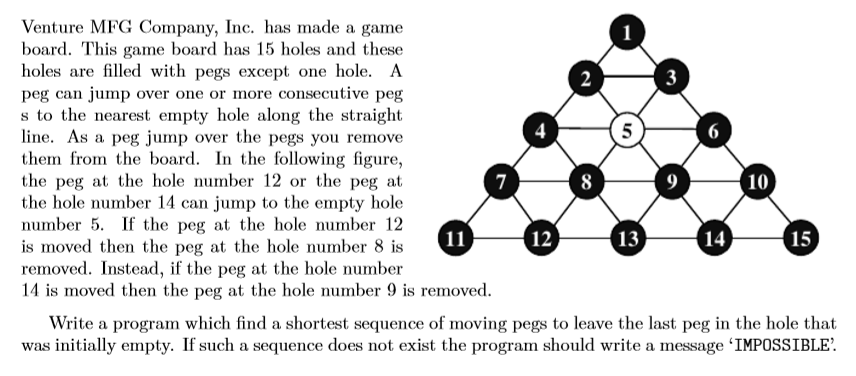
 Input

The input consists of T test cases. The number of test cases (T) is given in the first line of the input file. Each test case is a single integer which means an empty hole number.

 

 Output

For each test case, the first line of the output file contains an integer which is the number of jumps in a shortest sequence of moving pegs. In the second line of the output file, print a sequence of peg movements. Apegmovementconsistsofapairofintegersseparatedbyaspace. Thefirstintegerofthe pair denotes the hole number of the peg that is moving, and the second integer denotes a destination (empty) hole number.

 

 Sample Input

1

5

 

 

 Sample Ouput

10

12 5 3 8 15 12 6 13 7 9 1 7 10 8 7 9 11 14 14 5

 

题解：15个洞，二进制存储状态是比较正的思路。接下来就是水题了，只不过是把矩形地图换成了三角形地图，预处理一个临接表，存一下对于每个点能到哪些点。因为要字典序，因此顺序很重要，稍加分析就知道周围6个位置的大小关系，注意对于15个记录相邻点的数组，一定要统一顺序，除了字典序，还因为有可能要顺着一个方向走几格，这时顺序一致就很方便。

 

  1 #include <bits/stdc++.h>
  2 
  3 using namespace std;
  4 
  5 const int maxn = 15, maxm = 6;
  6 const int dir[maxn][maxm] = 
  7 {    
  8     {-1,-1,-1,-1, 1, 2},  {-1, 0,-1, 2, 3, 4},  { 0,-1, 1,-1, 4, 5},  {-1, 1,-1, 4, 6, 7},
  9     { 1, 2, 3, 5, 7, 8},  { 2,-1, 4,-1, 8, 9},  {-1, 3,-1, 7,10,11},  { 3, 4, 6, 8,11,12},
 10     { 4, 5, 7, 9,12,13},  { 5,-1, 8,-1,13,14},  {-1, 6,-1,11,-1,-1},  { 6, 7,10,12,-1,-1},
 11     { 7, 8,11,13,-1,-1},  { 8, 9,12,14,-1,-1},  { 9,-1,13,-1,-1,-1} 
 12 };
 13 
 14 
 15 int s;
 16 bool vis[1 << maxn];
 17 pair<int, int> path[1 << maxn];
 18 int pre[1 << maxn];
 19 
 20 struct Node {
 21     int sit, time;
 22     int pos;
 23     Node(int sit = 0, int time = 0, int pos = 0) :
 24         sit(sit), time(time), pos(pos) {}
 25 };
 26 
 27 int bfs(int &p) {
 28     int cnt = 0;
 29     int ori = (1 << maxn) - 1;
 30     ori ^= (1 << s);
 31     queue<Node> que;
 32     que.push(Node(ori, 0, 0));
 33     vis[ori] = true;
 34     while (!que.empty()) {
 35         Node first = que.front();
 36         que.pop();
 37         if (first.sit == (1 << s)) {
 38             p = first.pos;
 39             return first.time;
 40         }
 41 
 42         int ssit = first.sit;
 43         for (int i = 0; i < maxn; i++) {
 44             if (!(ssit&(1 << i))) continue;
 45 
 46             for (int j = 0; j < maxm; j++) {
 47                 int Next = dir[i][j];
 48                 if (Next == -1 || !(ssit&(1 << Next))) continue;
 49 
 50                 int tmp = ssit ^ (1 << i);
 51                 while (Next != -1) {
 52                     if (!(ssit&(1 << Next))) {
 53                         //printf("%d %d\n",i, Next);
 54                         tmp ^= (1 << Next);
 55                         if (!vis[tmp]) {
 56                             Node temp(tmp, first.time + 1, ++cnt);
 57                             pre[cnt] = first.pos;
 58                             path[cnt] = make_pair(i, Next);
 59                             que.push(temp);
 60                             vis[tmp] = true;
 61                         }
 62                         break;
 63                     }
 64                     tmp ^= (1 << Next);
 65                     Next = dir[Next][j];
 66                 }
 67             }
 68         }
 69     }
 70     return -1;
 71 }
 72 
 73 void output(int pos) {
 74     if (!pre[pos]) {
 75         printf("%d %d", path[pos].first + 1, path[pos].second + 1);
 76         return;
 77     }
 78     output(pre[pos]);
 79     printf(" %d %d", path[pos].first + 1, path[pos].second + 1);
 80 }
 81 
 82 int main()
 83 {
 84     int iCase;
 85     scanf("%d", &iCase);
 86     while (iCase--) {
 87         scanf("%d", &s);
 88         s--;
 89         memset(vis, false, sizeof(vis));
 90         memset(pre, -1, sizeof(pre));
 91         int pos;
 92         int ans = bfs(pos);
 93         if (ans == -1) {
 94             printf("IMPOSSIBLE\n");
 95         }
 96         else {
 97             printf("%d\n", ans);
 98             output(pos);
 99             printf("\n");
100         }
101     }
102     return 0;
103 }

 

转载于:https://www.cnblogs.com/npugen/p/9600814.html